| Головна |
| «« | ЗМІСТ | »» |
|---|
За умови надлишку субстрату швидкість реакції прямо пропорційна концентрації ферменту:
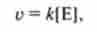
де і - швидкість реакції; | Е | - концентрація ферменту; до - константа швидкості реакції.
На рис. 6.4 представлено вплив концентрації ферменту аргінази на швидкість розщеплення аргініну. Відхилення від прямо пропорційній залежності можливо в разі дефіциту субстрату або коферменту (стосовно до відповідних складним ферментам), наявності в реакційній середовищі токсичних домішок.
Одним з найбільш важливих факторів, що впливають на швидкість ферментативних реакцій, є концентрація субстрату.
У більшості випадків графік залежності швидкості ферментативної реакції від концентрації субстрату являє собою гіперболу (рис. 6.5).
Криву можна розбити на дві ділянки: ділянку, на якому відповідно до закону діючих мас швидкість реакції пропорційна концентрації реагуючих речовин, і ділянку, на якому швидкість реакції не залежить від концентрації субстрату, вона постійна і максимальна.
Числове значення субстрату, при якому швидкість реакції дорівнює половині максимальної швидкості, називається константою Міхаеліса Дом.
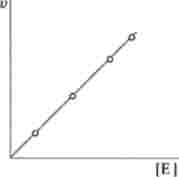
Мал. 6.4. Залежність швидкості реакції v від концентрації ферменту Е
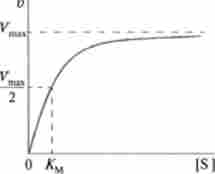
Мал. 6.5. Залежність між швидкістю реакції та концентрацією субстрату
Основні положення ферментативної кінетики, засновані на взаєминах між ферментами і різними концентраціями субстратів, були розроблені ще в 1913 р Л. Міхаелісом і М. Мснтсн. Запропоновані ними рівняння, що зв'язують швидкість реакції з концентрацією субстрату, в подальшому незначно видозмінювалися, однак загальні принципи залишилися непорушними. Згідно з цими принципами, фермент Е і субстрат S вступають в реакцію зі швидкістю, константа якої позначається до+]. При цьому утворюється комплекс ES, здатний диссоциировать на вихідні фермент і субстрат зі швидкістю, константа якої позначається к_}. У разі ж продуктивної ферментативної реакції з цього комплексу зі швидкістю до+2 виділяються фермент і продукти перетворення субстрату. Моносубстратную ферментативну реакцію можна записати в такий спосіб:
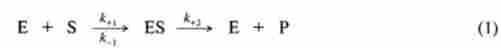
де Р - продукти перетворення субстрату.
У момент часу t концентрація вільного ферменту буде дорівнює | Е01 - | ES). Якщо концентрація субстрату набагато більше, ніж концентрація ферменту, що входить до складу фермент-субстратного комплексу, то змістом субстрату в цьому комплексі можна знехтувати. У цьому випадку швидкість утворення фермент-субстратного комплексу буде дорівнює:
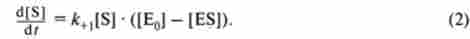
Поряд з утворенням фермент-субстратного комплексу можлива його дисоціація зі швидкістю на фермент і вихідний субстрат, а також розпад з утворенням продуктів реакції, що протікає зі швидкістю до+2. Цей процес описується рівнянням
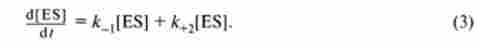
У стані рівноваги швидкість утворення комплексу і його розпаду дорівнює, отже:
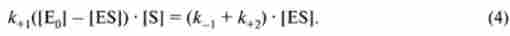
Після ряду спрощень отримуємо:

Л. Міхаеліс та М. Ментен постулювали, що швидкість реакції визначається як швидкість розпаду фермент-субстратного комплексу (константа швидкості дорівнює до+2). отже:

Підставляючи замість [ESJ його значення, з рівняння (5) отримуємо:

Спростити це рівняння можна наступним чином: позначимо?+2[Е0] як УТаху т. е. швидкість реакції в умовах, коли весь фермент пов'язаний з субстратом, а (А:+2 + ?_,) /? +, Як константу Міхаеліса Дом. При підстановці цих величин в рівняння (7) отримуємо:

Рівняння (8) є основним рівнянням Міхаеліса-Ментен стосовно моносубстратним ферментативним реакцій. Це рівняння пов'язує між собою початкову швидкість реакції, максимальну швидкість реакції і вихідну концентрацію субстрату. У разі, якщо початкова швидкість реакції дорівнює половині максимальної швидкості реакції, рівняння (8) набирає вигляду:

Розділивши обидві частини рівняння на Дотах, отримуємо:

Вирішуючи рівняння (10) щодо Х "м, отримуємо, що Дом одно | S |.
Отже, константа Міхаеліса чисельно дорівнює такій концентрації субстрату, при якій швидкість ферментативної реакції дорівнює половині максимальної.
Константа Міхаеліса має велике значення при дослідженні ферментів; вона є дуже важливим параметром, що характеризує, зокрема, ступінь спорідненості ферменту до субстрату.
Вираз, зворотне рівняння (8), являє собою:

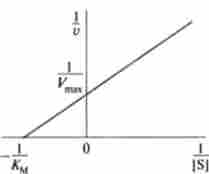
Мал. 6.6. визначення Дом і У ^ методом подвійних зворотних величин
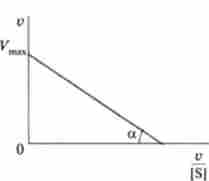
Мал. 6.7. визначення Дом і У ^ метолом Елі-Хофсті
Це лінійне рівняння Лайнуівера-Берка, завдяки якому можна поставити діагноз в одному експерименті константу Міхаеліса і максимальну швидкість досліджуваної ферментативної реакції.
У графічному вигляді метод Лайнуівера і Берка називають еше методом подвійних зворотних величин (рис. 6.6). При побудові графіка на осі абсцис відкладають величину, рівну 1 / | S |, а на осі ординат - 1 / Утлх.
У деяких випадках для визначення константи Міхаеліса і максимальної швидкості реакції більш перспективним є метод Еді-Хофсті. При використанні цього методу на осі ординат відкладають v, на осі абсцис - v / S. Отримана пряма лінія відсікає на осі ординат відрізок, рівний Дотах, а з віссю абсцис утворює кут а, тангенс якого дорівнює Vmax / tfN1 (Рис. 6.7).