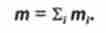
| Головна |
| «« | ЗМІСТ | »» |
|---|
Процеси життєдіяльності на Землі обумовлені значною мірою накопиченням сонячної енергії в біогенних речовинах - білках, жирах, вуглеводах - і подальшими перетвореннями цих речовин в живих організмах - рослинах і тварин з виділенням енергії.
Особливо чітко розуміння взаємозв'язку хімічних перетворень і енергетичних процесів в організмі було усвідомлено після досліджень, проведених спільно великими французькими дослідниками природи Антуаном Лавуазьє (1743-1794) і П'єром Лапласом (1749-1827). Ці вчені за допомогою придуманого ними калориметр прямими вимірами на тваринах показали, що енергія життєдіяльності визначається окисленням продуктів харчування киснем повітря, вдихуваним тваринами.
Бурхливий розвиток машинобудування в XIX-XX ст. привело до створення нової науки - термодинаміки.
Термодинаміка (від грец. «Therme» - тепло і «dynamikos» - сильний) - наука про взаимопревращениях теплоти і енергії.
Біоенергетика - розділ термодинаміки, що вивчає взаємозв'язок між обміном речовин і енергії в живих системах
За допомогою методів термодинаміки стало можливо кількісно строго розраховувати перетворення енергії не тільки в теплових машинах, але і в біохімічних реакціях і фізіологічних процесах, передбачати їх напрямок.
Термодинамічні методи засновані на ряді строгих понять: «система», «стан системи», «внутрішня енергія системи», «функція стану системи».
Термодинамічної системою називають будь-який об'єкт природи, що складається з досить великого числа молекул (структурних одиниць) і відокремлений від інших об'єктів природи реальної чи уявної граничної поверхнею (межею поділу).
З даного визначення випливає, що до термодинамічних систем можуть бути віднесені і такі величезні об'єкти природи, як зірки, і найменші живі істоти - мікроорганізми. Звідси зрозуміло, наскільки важливо знати закони термодинаміки.
Об'єкти природи, що не входять в систему, називають середовищем.
Середовищем для нашої планети є Всесвіт. Середовищем для мікроорганізму в чашці Петрі є агар з поживною сумішшю речовин.
Найбільш загальними характеристиками самих різних систем є маса т речовини, що міститься в системі, і внутрішня енергія Е системи.
Маса т речовини системи є величина, яка вимірюється сумою мас т, молекул (структурних одиниць), з яких вона складається:
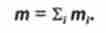
Внутрішня енергія Е системи є величина, яка вимірюється сумою енергій теплового руху Е "молекул і енергій
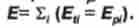Еи взаємодії між ними:
Системи за характером обміну речовиною і енергією з навколишнім середовищем (зовнішніми об'єктами природи) поділяють на три типи: ізольовані (Рис. 5.1, а), закриті (Рис. 5.1, б) і відкриті (Рис. 5.1, в).
Ізольованою системою називається така система, яка не обмінюється із середовищем ні речовиною, ні енергією [Ат = О, АЕ = 0).
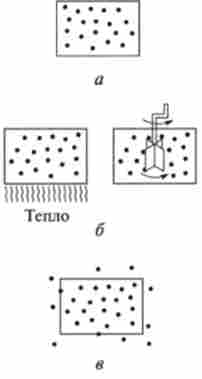
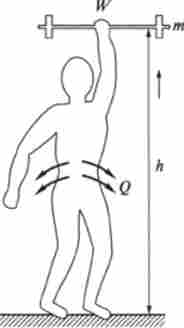
Мал. 5.1. Типи термодинамічних систем:
а - ізольовані, б - закриті, в відкриті
Мал. 5.2. Термодинаміка процесів при здійсненні людиною механічної роботи підняття тяжкості:
W - механічна робота. Q - теплота при піднятті людиною гантелі масою т на висоту І
Прикладами практично ізольованих систем можуть служити побутової термос, судини Дьюара для тривалого зберігання при низьких температурах життєздатних організмів.
Закритою системою називають таку систему, яка не обмінюється із середовищем речовиною, але може обмінюватися енергією [Ат = 0, АЕ * 0).
Обмін енергією в закритих системах може здійснюватися шляхом передачі теплоти Q або здійснення роботи IV.
Прикладом закритої системи може служити герметично закриту посудину з мішалкою для вирощування мікроорганізмів в термостаті, що підтримує задану температуру.
Відкритою системою називають таку систему, яка може обмінюватися з середовищем і речовиною і енергією (Ат Ф 0, АЕ Ф 0).
Прикладами відкритої системи є жива клітина, організм людини. Прикладом з побуту може служити пральна машина.
Одне з найважливіших понять - «стан системи».
Під станом системи розуміють сукупність властивостей системи, що дозволяють визначити цю систему з точки зору термодинаміки.
Кількісно стану розрізняють за допомогою термодинамічних змінних (або параметрів).
Термодинамічними змінними називають такі властивості системи, значення яких характеризують стан системи в цілому.
Найважливішими термодинамичними змінними є: тиск р, температура Г, обсяг системи V або загальна маса системи / і, маса хімічних речовин (компонентів) т*, З яких складається система, або концентрація цих речовин з *.
Слід зазначити, що аналогічні характеристики (температура і маса тіла, склад біологічних рідин організму - аналізи, артеріальний тиск) використовуються в медицині для визначення стану пацієнта.
Процесом називається перехід системи з одного стану в інший.
В результаті процесу стан системи і термодинамічні змінні змінюються. Ці зміни кількісно характеризуються різницею термодинамічних змінних в початковому і кінцевому станах, між якими здійснюється перехід в даному процесі.
У термодинаміки для визначення зміни енергії системи в тих чи інших умовах застосовують різні енергетичні характеристики.
Внутрішня енергія системи Е - одна з енергетичних функцій стану. Зміна внутрішньої енергії системи АЕ може бути обумовлено роботою W% яка відбувається при взаємодії системи з середовищем, і передачею теплоти Q між середовищем і системою. Співвідношення між цими величинами становить зміст 1-го початку термодинаміки.
Приріст внутрішньої енергії системи ДЕ в деякому процесі одно теплоті О, отриманої системою, плюс робота IV, досконала над системою в
цьому процесі:
У біологічних системах теплота зазвичай віддається системою в зовнішнє середовище, а робота здійснюється системою за рахунок убутку внутрішньої енергії (рис. 5.2). Тому математичний запис першого закону термодинаміки зручно представити у вигляді
а 1-е початок термодинаміки формулюється так:
Спад внутрішньої енергії системи ДЕ в деякому процесі дорівнює теплоті О, відданої системою, мінус робота IV, здійснена системою в цьому процесі.
Всі величини в наведених формулах вимірюються в джоулях (Дж).
В якості ілюстрації, що дає уявлення про застосування 1-го початку термодинаміки, зручно розглянути зв'язок між теплотою, роботою і внутрішньою енергією при багаторазовому піднятті вантажу людиною (рис. 5.2).
Завдання. Відомо, що максимальна механічна робота, яка може бути здійснена людиною в результаті окислення 1 г глюкози киснем (з урахуванням ККД живого організму г ~ 40%), дорівнює 6,5 кДж / г. При цьому виділяється теплота, що дорівнює Qp = 9,5 кДж / г. Яка маса глюкози повинна окислюватися в м'язах, щоб людина могла підняти 25 разів вантаж масою т = 20 кг на висоту І- 2 м?
Рішення. Відповідно до законів фізики механічна робота з підняття вантажу lV = vntgh, де v - число підняттів, т. е. 1Т = -10кДж. Отже, для здійснення цієї роботи в м'язах окислюється приблизно
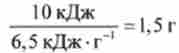глюкози і виділяється теплота Q = -9,5 кДж / гх
х1,5 г = -14,3 кДж. Таким чином, відповідно до 1-м початком термодинаміки спад внутрішньої енергії організму в результаті окислення глюкози становить АЕ = -14,3 кДж - 10 кДж = -24,3 кДж.
Цей простий приклад показує, що на основі 1-го початку термодинаміки за допомогою нескладних розрахунків можна отримати важливу інформацію про процеси обміну речовин і енергії в організмі.
Німецький лікар Ю. Р. Майєр вперше сформулював 1-е початок термодинаміки (1840), виходячи зі спостережень таких процесів у людини. Вихідними роботами, який послужив основою застосування цього закону до хімічних реакцій, з'явилися дослідження російського вченого Г. І. Гесса (1840), а остаточним його підтвердженням стали експериментальні дослідження англійського фізика Д. Джоуля (1850).
1-е початок термодинаміки відноситься до числа фундаментальних законів природи, які не можуть бути виведені з якихось інших законів. Справедливість 1-го початку термодинаміки доводять численні експерименти. До них відносяться експерименти з негативним результатом - невдалі спроби побудувати вічний двигун першого роду, т. Е. Таку машину, яка змогла б як завгодно довго здійснювати роботу без підведення енергії ззовні. Слід пам'ятати також, що 1-е початок термодинаміки є кількісним виразом одного з найважливіших законів природи про незнищенність матерії і її руху.
Організм робить роботу, витрачаючи внутрішню енергію, накопичену в вигляді енергії хімічної взаємодії атомів складових його речовин. Математичний вираз (5.2) 1-го початку термодинаміки визначає точне співвідношення між витратою внутрішньої енергії системи Л ?, роботою W, яку здійснюють системою, і енергією Q, яка втрачається у вигляді теплоти. Однак з 1-го початку термодинаміки можна визначити частину витрачається внутрішньої енергії, яка може бути перетворена в роботу. Правда, при розрахунку, наприклад, витрат енергії при здійсненні механічної роботи (рис. 5.2) враховувалися теплові втрати. Але звідки береться значення цих втрат?
Найбільш загальним методом експериментального визначення ефективності витрат внутрішньої енергії організмом є калориметричні вимірювання, що застосовуються фізіологами, а також ергометрічні.
Теоретичні оцінки витрат здійснюються на основі 2-го початку термодинаміки. Цей закон накладає суворі обмеження на ефективність перетворення енергії в роботу і, крім того, дозволяє ввести критерії можливості самовільного протікання того чи іншого процесу.
Процес називається мимовільним, якщо він здійснюється без будь-яких впливів, коли система надана самій собі.
Людина, що знає загальний закон збереження енергії з фізики, але не знайомий з термодинаміки, може припустити, що хімічні і фізичні процеси можуть протікати мимовільно лише зі зменшенням внутрішньої енергії системи. Таким чином, передбачається, що критерієм самопроизвольности служить негативне значення приросту внутрішньої енергії (АЕ 0).
Таке припущення може бути засноване, зокрема, на спостереженнях за рухом предметів у земної поверхні. Всі добре знають, що предмети падають зверху вниз, а не навпаки. З фізики відомо, що при цьому зменшується потенційна енергія? піт тіла, т. е. має місце спад потенційної енергії (AEnoi < 0). Однак вивчення різних процесів, в тому числі хімічних реакцій, показало, що правило зменшення внутрішньої енергії (АЕ 0) не завжди доречно.
По-перше, існують процеси, при яких внутрішня енергія системи не змінюється (АЕ - 0). До таких процесів відноситься, наприклад, іонізація оцтової кислоти у воді.
По-друге, ряд мимовільних процесів протікає зі збільшенням внутрішньої енергії (АЕ> 0). До них відносяться, зокрема, типові реакції освіти біонеорганічної з'єднань альбуміну (білок плазми крові) з іонами металів, наприклад Сі2*.
Існує, звичайно, безліч мимовільних процесів, що відбуваються зі зменшенням внутрішньої енергії (АЕ 0), наприклад реакції окислення органічних сполук, в тому числі реакція окислення глюкози при клітинному диханні.
Таким чином, зміна внутрішньої енергії АЕ для закритих систем не може служити критерієм мимовільного протікання процесів. Отже, 1-го початку термодинаміки, з якого отримано цей критерій, недостатньо для вирішення питання про самопроизвольности, так само як і про ефективність процесів. Вирішення цих питань досягається за допомогою 2-го початку термодинаміки.
Для формулювання 2-го початку термодинаміки необхідно ввести поняття оборотного і необоротного в термодинамічній сенсі процесів.
При зміні зовнішніх умов стан системи може змінюватися, т. Е. В системі може протікати процес. Якщо, наприклад, система укладена в циліндр, то зміна зовнішнього тиску викликає процес, що приводить до зміни обсягу системи, і система переходить зі стану 1 з об'ємом V в стан 2 з об'ємом * 2.
процес називається термодинамічно оборотним, якщо при переході з початкового стану 1 в кінцевий стан 2 всі проміжні стану виявляються рівноважними.
Оборотний процес на будь-якому етапі можна змусити йти в зворотному напрямку, змінивши зовнішні умови на дуже малу величину. Наприклад, при оборотному розширенні газу можна почати стиснення в довільний момент шляхом збільшення тиску р на нескінченно малу величину dp.
процес називається термодинамічно незворотних, якщо хоч одне з проміжних станів нерівноважної.
Оборотний процес можна здійснити лише при досить повільному зміні параметрів системи - температури, тиску, концентрації речовин і ін. Швидкість зміни параметрів повинна бути такою, щоб виникаючі в ході процесу відхилення від рівноваги були пренебрежимо малі. Слід зазначити, що з оборотністю пов'язана важлива проблема медицини - консервація тканин при низьких температурах.
Зворотні процеси є граничним випадком реальних процесів, що відбуваються в природі і здійснюються в промисловості або в лабораторіях.
Максимальна робота яка може бути отримана при даній убутку
внутрішньої енергії ДЕ в процесі переходу зі стану 1 в стан 2, досягається лише в тому випадку, якщо цей процес оборотний. Відповідно до виразом (5.1) для 1-го початку термодинаміки при цьому виділяється мінімальна теплота QMHH
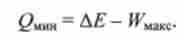
Максимально досяжний коефіцієнт корисної дії, що характеризує ефективність витрат внутрішньої енергії системи, відповідно дорівнює
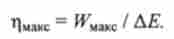
При необоротний процес переходу зі стану 1 в стан 2 вироблена системою робота менше WMWQ. Щоб розрахувати т)макс при відомому значенні Д ?, необхідно знати величину WMUX або
величину QMHM визначають на основі 2-го початку термодинаміки за допомогою термодинамічної функції стану, званої ентропією.
Поняття ентропії ввів (1865) німецький фізик Р. Ю. Клаузиус (1822-1888) - один із засновників термодинаміки і молекулярно-кінетичної теорії теплових процесів. На основі цього поняття Р. Ю. Клаузиус одночасно з У. Томсоном в 1850 р дав перше формулювання 2-го початку термодинаміки. Відповідно до Клаузиусом
ентропія - це функція стану, приріст якої AS одно підведеної до системи в оборотному ізотермічному процесі теплоті Омін1 поділеній на абсолютну температуру Т, при якій здійснюється процес:
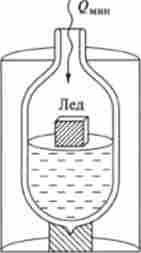
Мал. 5.3. Оборотне плавлення (танення) льоду в термосі з водою при Тм = 273 К
З формули (5.3) випливає, що одиниця СІ вимірювання ентропії - Дж / К.
Прикладом оборотного ізотермічного процесу може служити повільне танення льоду в термосі з водою при 273 К (рис. 5.3). Експериментально встановлено, що для плавлення 1 благаючи льоду (18 г) необхідно підвести принаймні 6000 Дж теплоти. При цьому ентропія системи лід-вода в термосі зростає на ДS = 6000: 273 = 22 Дж / К.
При охолодженні води в термосі при 273 К можна повільно відвести 6000 Дж теплоти. В результаті відбувається при цьому кристалізації води утворюється 1 моль льоду. Для цього процесу величина QMHH у формулі (5.3) має від'ємне значення. Відповідно ентропія системи лід-вода при утворенні 1 благаючи льоду зменшується на ДS = -22 Дж / К.
Аналогічним чином можна розрахувати зміна ентропії при будь-яких ізотермічних фізичних і хімічних процесах, якщо відома теплота?хв, підводиться до системи або відведена від неї при цих процесах. Як відомо з фізики, ця теплота може бути визначена за допомогою калориметричних вимірів.
Таким чином, зміна ентропії, як і двох інших функцій стану системи - внутрішньої енергії та ентальпії, являє собою експериментально визначається величину. Фізичний сенс ентропії, як і внутрішньої енергії, чітко виявляється при розгляді з молекулярно-кінетичної точки зору процесів, що протікають в ізольованих системах.
Ізольовані системи, за визначенням, не обмінюються із зовнішнім середовищем ні речовиною, ні енергією. Звичайно, реально таких систем в природі не існує. Однак дуже хороша ізоляція може бути здійснена, якщо помістити систему в термос із закритою пробкою.
Як приклад теплоизолированной системи розглянемо термос з двома шарами рідин. Нижній шар - пофарбований сироп, а верхній, безбарвний шар - газована вода (рис. 5.4, а). Добре відомо, що після досить великого проміжку часу межа між шарами зникне і в термосі вийде однорідний за кольором розчин - «коктейль». Очевидно, що в результаті теплового руху частинок відбувається дифузія компонентів і вони рівномірно розподіляються по системі. Після цього в системі встановлюється рівновага, яке зберігається до тих пір, поки підтримується ізоляція.
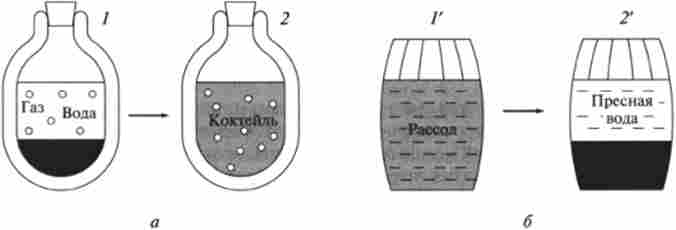
Мал. 5.4. Процеси перерозподілу речовини: а - мимовільний процес вирівнювання концентрацій в ізольованій двошарової системі.
6 - мимовільне гіпотетичне опріснення; /, / '-Ісходние стану, 2, 2' кінцеві стану
Оскільки система ізольована, обмін енергією шляхом передачі теплоти, речовини і здійснення роботи не відбуваються. Отже, термодинамічна функція - внутрішня енергія Е системи - не змінюється. У той же час очевидно, що стан системи змінилося, так як компоненти всередині неї перераспределились. Ця зміна - мимовільний перехід з двошарового стану 1 з ентропією S в стан 2 однорідного розчину з ентропією S2 (Рис. 5.4, а) - як раз і характеризується збільшенням ентропії: ДS = S2~ S.
Будь мимовільний процес може протікати в ізольованій системі
лише в тому випадку, якщо він характеризується збільшенням ентропії; в рівновазі ентропія системи постійна:
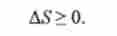(5.4)
Це твердження, засноване на експериментальних спостереженнях, є однією з можливих формулювань 2-го початку термодинаміки.
Процес, зворотний мимовільного, згідно 2-му закону термодинаміки в ізольованій системі протікати не може, оскільки такий процес характеризується зменшенням ентропії. Зокрема (рис. 5.4, а), з повсякденного досвіду добре відомо, що зворотний процес переходу від рівномірно забарвленого розчину - «коктейлю» (стан 2) до двошарової системі (стан 1) не відбувається. Здійснення такого процесу означало б, наприклад, можливість самовільного опріснення в бочці з солоною водою (рис. 5.4, б). Хоча в принципі такий процес не суперечить 1-му закону термодинаміки, неважко уявити, що в результаті теплового руху іони солей зберуться в одній половині судини.
У молекулярних системах число можливих розташувань молекул величезна і швидко зростає зі збільшенням кількості речовини і розмірів системи. Вельми істотно, що будь-якому з цих розташувань відповідає одне і те ж значення внутрішньої енергії Е системи. Внутрішня енергія, за визначенням, складається з енергій індивідуальних молекул, або, як кажуть у фізиці, внутрішня енергія розподіляється по окремим молекулам і різним розташуванням.
Кожному розташуванню молекул відповідають різні розподілу внутрішньої енергії Е системи за складовими її часткам. Очевидно, що чим більше варіантів розподілу цієї енергії, тим більше невпорядкованості хаотична система. На цій підставі австрійський фізик Л. Больцман в 1872 році запропонував статистичну трактування поняття ентропії системи:
"? Ентропія системи є міра невпорядкованості, хаотичності системи.
На основі статистичної трактування Больцмана можна теоретично розрахувати абсолютні значення ентропії кристалізуються речовин, на відміну від внутрішньої енергії?, Для якої можна визначити лише відносні значення.
Важливе значення поняття ентропії пов'язане з тим, що на основі цієї величини можна прогнозувати напрям самовільного протікання процесів. Однак застосовність зміни ентропії як критерій спрямованості процесів обмежується ізольованими системами відповідно до формулюванням
2-го початку термодинаміки (5.4).
Для неізольованих, т. Е. Закритих і відкритих, систем зміна ентропії, як і зміна внутрішньої енергії, вже не є критерієм самопроизвольности.
Приклад 1. При кристалізації води з утворенням льоду в закритій посудині (див. Рис. 5.3) вода в результаті тепловіддачі в навколишнє середовище переходить з невпорядкованого рідкого стану в упорядковане кристалічна. При цьому освіту кожних 18 г (1 моль) льоду супроводжується зменшенням ентропії системи ДS = -22 кДж / К, т. Е. Хоча процес мимовільний, ентропія убуває на AS < 0. Однак спад ентропії суперечить формулюванні 2-ix> початку термодинаміки (5.4), оскільки вона справедлива тільки для ізольованих систем.
Як критерій самопроизвольности процесів у відкритих і закритих системах вводиться функція стану - енергія Гіббса. Ця функція отримала назву на честь великого американського фізика Д. У. Гіббса (1839-1903), який використовував її для опису властивостей термодинамічних систем.
енергія Гіббса G визначається через внутрішню енергію Е і ентропію S за допомогою співвідношення
Якщо процес протікає оборотно при постійних тиску р і температурі Т (Такі процеси називають ізобарно-ізотермічними), відповідне прирощення енергії Г Іббсе одно
На основі енергії Г Іббсе 2-е початок термодинаміки можна сформулювати наступним чином.
-? В ізобарно-ізотермічних умовах (р, Г = const) в системі мимовільно можуть здійснюватися тільки такі процеси, в результаті яких енергія Гіббса системи зменшується (AG < 0). У стані рівноваги енергія Гіббса системи не змінюється (G = const, AG = 0):
У розглянутих вище прикладах іонізації оцтової кислоти, реакціях альбуміну і окислення органічних сполук енергія Гіббса системи зменшується (AG < 0) і процеси здійснюються мимовільно. Зміна внутрішньої енергії АЕ має при цьому різні знаки. Виходячи з виразу (5.6), можна зробити висновок, що в перших двох випадках ентропія системи зростає (А5> 0).
Енергія Гіббса дозволяє вирішити питання про розрахунок максимальної роботи 1Гмакс, яку може зробити система, витрачаючи внутрішню енергію АЕ, і розрахувати теоретичний коефіцієнт корисної дії timbkc = WMMJAE. Це особливо важливо для оцінки навантажень, раціону харчування при фізичних вправах і прогнозування напрямку мимовільних процесів в організмі.
Виходячи з математичних виразів (5.1) і (5.4) для 1-го і 2-го почав термодинаміки, можна довести таке положення.
-? В ізобарно-ізотермічних умовах (р, Т = const) максимальна робота -1VMMC, яка може бути здійснена системою в даному процесі понад роботи розширення, дорівнює убутку енергії Гіббса -AG, якщо процес оборотний, і менше -AG, якщо процес незворотний:
величина WUMC за абсолютним значенням дорівнює повній роботі, яка може бути здійснена системою при даному процесі, за вирахуванням роботи розширення, що дорівнює pAV. З урахуванням нерівності (5.8) максимально досяжний при оборотному процесі коефіцієнт корисної дії дорівнює
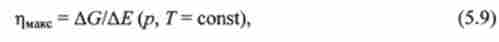
де AG і АЕ - зміни енергії Гіббса і внутрішньої енергії системи при навантаженні.
Коефіцієнт корисної дії при довільному ізобарно-ізотермічному процесі підпорядковується нерівності
Нерівність (5.10) може служити ще одним математичним виразом 2-го початку термодинаміки для неізольованих систем.
З викладеного випливає, що енергія Гіббса G відіграє велику роль для вивчення біоенергетичних процесів. За допомогою цієї функції стану можна прогнозувати напрям мимовільних процесів в біологічних системах і розраховувати максимально досяжний ККД.
енергія Гіббса G є функцією (енергетичної) стану системи, тому її зміна AG може використовуватися для характеристики хімічних перетворень. Рівняння реакцій, для яких вказується відповідне цим реакцій зміна енергії Гіббса, називаються термохімічними.
Хімічні реакції, при протіканні яких відбувається зменшення енергії Г Іббсе системи (AG 0) і здійснюється робота, називаються екзергонічеськие. Реакції, в результаті яких енергія Г Іббсе зростає (АТ ' > 0) і над системою здійснюється робота, називаються ендергоіічними. екзергонічеськие реакції лежать в основі енергетичного забезпечення життєдіяльності організму, в тому числі фізичних навантажень.
Приклад 2. Окислення глюкози СБН ^ Про дікіслородом Ог супроводжується зменшенням енергії Г Іббсе A G = -2880 кДж / моль, т. Е. Цей процес екзергоні- ний. Саме в результаті цієї реакції здійснюються різні види роботи в організмі людини. За допомогою формули (5.9) можна розрахувати максимальний коефіцієнт корисної дії даного процесу.
Спад внутрішньої енергії системи в результаті окислення глюкози приблизно дорівнює убутку ентальпії: АЕ ~ Qcrop = -2880 кДж / моль (Qcгор - теплота згоряння глюкози). Отже, відповідно до формули (5.9) максимальний коефіцієнт корисної дії дорівнює
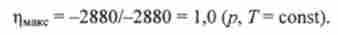
В дійсності ц дорівнює приблизно 0,4, т. е. приблизно 60% енергії, запасеної в глюкозі, розсіюється у вигляді теплоти (див. рис 5.2).
Оскільки виведена на основі 2-го початку термодинаміки енергія Гіббса є функцією стану, то на основі 1-го початку термодинаміки може бути сформульований закон Гесса для енергії Г Іббсе в наступній формі.
-^ -Зміна енергії Гіббса в реакції AG ^., Освіти заданих продуктів з
даних реагентів при постійних тиску і температурі не залежить від числа
і виду реакцій, в результаті яких утворюються ці продукти.
Саме на цьому законі заснований теоретичний розрахунок «калорійності» - енерговіддачі різних продуктів харчування за допомогою таблиць термодинамічних даних по теплоті згоряння і освіти різних речовин (див. Додаток).
Важливий приклад застосування закону Гесса - розрахунок енергії Гіббса реакції окислення глюкози СБН ^ Про дікіслородом О2. Зміна енергії Гіббса в цій реакції при р = 101кПа і Т = 298 К, певне поза організмом, так само
AG ° = -2880 кДж / моль. Відповідне термохімічне рівняння записується у вигляді
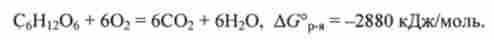
У клітинах організму ця реакція здійснюється через ряд послідовних стадій, вивчених биохимиками. Можна передбачити, виходячи із закону Гесса, що сума змін енергій Гіббса у всіх проміжних реакціях дорівнює AG0p.,:
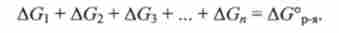
Це пророцтво добре узгоджується з експериментальними даними, що ілюструється діаграмою Гіббса (рис. 5.5, а). На цій діаграмі відкладені рівні енергії Гіббса, відповідні вихідним реагентів - глюкози і дікіслороду, а також проміжних продуктів - інтермедіатами: фруктозофосфа- ту, лактату, пірувату та ін. Відстань між рівнями визначається величинами AGi, AG2, AG3, ...
Сумарна висота енергетичних ступенів між початковим і кінцевим рівнями (висота сходів між нижнім і верхнім «поверхами») однакова незалежно від числа ступенів. Звідси можна зробити висновок, що для реакції а + ЬВ = сС + Сю справедливо наслідок закону Гесса для енергії Гіббса:
Енергія Гіббса реакції AGp. "Дорівнює сумі алгебри енергій Гіббса освіти стехіометричного кількості продуктів за вирахуванням алгебраїчної суми енергій Гіббса освіти стехіометричного кількості реагентів:
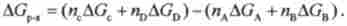
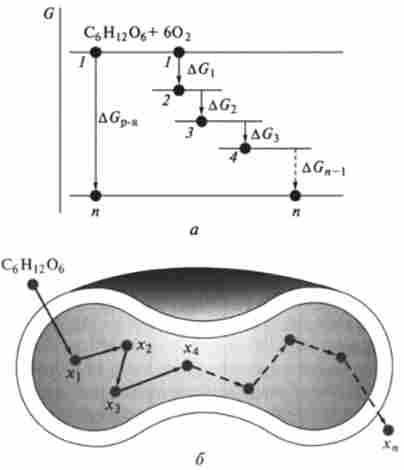
Мал. 5.5. Діафамма змін енергії Г Іббсе (А) в послідовних стадіях біоокислення глюкози в еритроциті (Б) (1-4 - рівні енергії системи)
Експериментально визначені ентальпії освіти Q, ° і енергії Гіббса AG / ° різних біогенних речовин X, в стандартних умовах (Р = 101 кПа, Т = 298 К) зведені в таблиці (табл. 5.1). За допомогою цих табличних даних на основі закону Гесса можна проводити біоенергетичні розрахунки для великого числа біохімічних реакцій і прогнозувати їх перебіг.
Таблиця 5.1
Стандартні значення теплоти освіти Про ", енергія Гіббса освіти AG ° і абсолютна ентропія S різних речовин при 298,1 К
|
речовина |
м К'Лж / М0.1Ь |
Л (7 °, кДж / моль |
5 °, Лж / (моль'К) |
речовина |
Qв. кДж / моль |
ЛЗ °, кДж / моль |
S°, Дж / (моль'К) |
|
Н * (водн.) |
0,0 |
0,0 |
0,0 |
З2Н2 (Г) |
227 |
209 |
201 |
|
Н30 * (водн.) |
-286 |
-237 |
69,9 |
З2Н4 (Г) |
52,3 |
68,1 |
220 |
|
Н2(Г) |
0,0 |
0,0 |
131 |
З2Н6(Г) |
-84,7 |
-32,9 |
230 |
|
Li (т) |
0,0 |
0,0 |
28,0 |
СБН6 (Ж) |
49,0 |
124 |
173 |
|
Li * (водн.) |
-278 |
-294 |
14 |
НСООН (Хвиль.) |
-410 |
-356 |
164 |
|
LiCl (т) |
-409 |
-384 |
55,2 |
НСОО (водн.) |
-410 |
-335 |
92 |
|
Na (т) |
0,0 |
0,0 |
51,0 |
Н2С03 (Водн.) |
-699 |
-623 |
191 |
|
Na * (водн.) |
-240 |
-262 |
60,2 |
НС03"(Водн.) |
-691 |
-587 |
95 |
|
Na20 (т) |
-416 |
-377 |
75 |
С032 (Водн.) |
-676 |
-528 |
-53 |
|
NaCI (т) |
-411 |
-384 |
72,4 |
СН3СООН (Водн.) |
-488 |
-400 |
- |
|
К (т) |
0,0 |
0,0 |
63,6 |
СН3СОО (Водн.) |
-486 |
-369 |
88 |
|
К * (водн.) |
-251 |
-282 |
103 |
СН3ВІН (ж) |
-239 |
-166 |
127 |
|
КС1 (т) |
-436 |
-408 |
82,7 |
З2Н5ВІН (ж) |
-278 |
-175 |
161 |
|
Mg (т) |
0,0 |
0,0 |
32,5 |
СН3СНТ (т) |
-166 |
-134 |
266 |
|
Mg2* (Водн.) |
-462 |
-456 |
-118 |
СБН |2Про (т) |
-1260 |
-919 |
289 |
|
MgCI2 (Т) |
-642 |
-542 |
89,5 |
РЬ2* (Водн.) |
1,6 |
-24,3 |
21 |
|
Са (т) |
0,0 |
0,0 |
41,6 |
NH3(R) |
-46,2 |
-16,6 |
192 |
|
Са2* (Водн.) |
-543 |
-553 |
-55,2 |
NH3 (Водн.) |
-80,8 |
26.6 |
ПО |
|
СаС12 (Т) |
-795 |
-750 |
114 |
NH4* (Водн.) |
-133 |
-79,5 |
113 |
|
CaCOj (т) |
-1207 |
-1129 |
92,9 |
NI14C1 (Т) |
-315 |
-204 |
95 |
|
Гс2>(Водн.) |
-87,9 |
-84.9 |
-113 |
nh2conh2 (Т) |
-333 |
-197 |
105 |
|
Fc3* (Водн.) |
-47,7 |
-10,6 |
-293 |
02(Г) |
0,0 |
0,0 |
205 |
|
Сі2* (Водн.) |
64,4 |
65,0 |
-98,7 |
03 (Г) |
142 |
163 |
238 |
|
CuS04 (Т) |
-770 |
-662 |
З |
ВІН (водн.) |
-230 |
-157 |
-10,5 |
|
А13* (Водн.) |
-525 |
-481 |
-313 |
Н20 (ж) |
-286 |
-237 |
70 |
|
А1СЬ (т) |
-653 |
-637 |
167 |
Н202 (Ж) |
-188 |
-114 |
92 |
|
С (т), графіт |
0,0 |
0,0 |
5,69 |
F (водн.) |
76,6 |
59,4 |
159 |
|
С (т). алмаз |
1,83 |
2,83 |
2,36 |
СГ (водн.) |
-167 |
-131 |
55 |
|
СО (г) |
-ПО |
-137 |
198 |
НС1 (водн.) |
-167 |
-131 |
55 |
|
С02 (Г) |
-393,5 |
-394,4 |
213,6 |
Г (водн.) |
-56 |
-52 |
109 |
|
С02 (Водн.) |
-413 |
-386 |
121 |
S042 (Водн.) |
-909 |
-744 |
18,2 |
|
СН4(Г) |
-74.8 |
-50,8 |
186 |
S (т), ромбіч. |
0,0 |
0,0 |
31,9 |