Пояснення

Поняття порожнечі в німецькій культурі таке, що повітря їй не заважає бути (а у Франції, в космогонії Декарта, наприклад, заважає). Повітря взагалі не заважає формі, вогні-землі: вони один в одному битій-обхідних привільно, дух і праця формування ; порожнеча і є свобода.

Вони разом протистоять стихії води, природи, як необхідності, нівелюванню і смерті.

Отже, порожній посудину мислиться як тіло з віз-духом всередині. Така порожнеча є небуття як потенція буття. У німецькій класичній філософії недарма в основу був покладений Дух, його хід по формам, речей, предметів та закінчення сенсу через них: кожна форма сочиться духом.

« Постулат VI. Верхня поверхня води є площина, паралельна горизонту »(122).

Зіставимо з вихідним пропозицією Архімеда:« Поверхность всякої рідини, що перебуває в спокої, має форму сфери, центр якої збігається з центром землі »(92).

У цьому вузлі і осередок відмінностей еллінського і німецького світогляду: вихідне для еллінства умогляд - куля, коло; германська ж культура прагне випрямити куля - в куб, коло - в квадрат, дугу - в малу пряму.

У «Пояснення» Стевін розтлумачує свій постулат так: «Відомо, що поверхня води має форму сфери, відповідної земної поверхні або їй концентрической, а також, що краплі води мають особливу форму поверхні »(123). Значить, визнається факт кулястості форми землі (макрокосмосу) і шарообразность краплі (мікрокосмосу). Але зізнається де факто, як результат досвіду, а не де юре, як наш можливий досвід, як апріорність властивих нам форм мислення, що дозволяють нам, що перебувають між нескінченно великим і нескінченно малим (між двома Паскалева безоднями), мислити реальне буття, всякий можливий досвід. І виходячи з апріорних форм духу, логічно знехтувати нескінченно малим. Це зробить винайдений пізніше в германства Ньютоном і Лейбніцем математичний аналіз, який, до речі, теж спонукуваний ворожнечею до кривих і прагне не розрізняти дугу від хорди і дотичною, випрямляє плазом її пресом, здавлюючи її знизу, від хорди, і зверху, від дотичній, тобто роблячи її «паралельної горизонту». Ось як робить це Стевін: «Наш постулат не поширюється на останні незначні кількості води (тобто на краплю. - Г. Г.), а проте це не має практичного значення» (123). Для еллінів важливо було теоретичне значення, чистота істини, і тому метод наближень і практичне самовдоволення тим, що нам по-ургіі, для праці підходить, цей прагматизм був би їм огидний і розглядався як помилковий принцип. «Що ж до сферичної форми поверхні води, відповідної земної поверхні, то прийняття відповідного положення надзвичайно ускладнило б доказ наступних пропозицій, не давши ніяких практичних вигод для гідростатики »(123).

Пригадаємо знову трактат Архімеда. У першому ж реченні він звертається до геометричних форм сфери та кола як до таких образів і інструментам, з якими йому найлегше, природніше і истиннее працювати, і все наступне міркування полягає у приведенні різних сюжетів з плаваючими тілами - до саме глобальному їх розгляду, виходячи з Цілого - СФЕРОС - нашої Землі і проводячи всі лінії до центру Землі. Така суть еллінського підходу - завжди виходити з Цілого певного світу - кулі. Тому й докази від протилежного можливі: як імпульси, вдаряються об стінку, а не йдуть непружно в нескінченність, як наші (радіо) хвилі ... Для Стевіна ж сфера і коло абсолютно не є інтимними, чужорідні, і хоча він змушений визнати їх як даності, але в конкретній роботі насамперед перетворює їх в рідні собі форми кубів, квадратів і прямих. «З метою спрощення міркувань ми приймаємо тому, що поверхня води є плоскою і паралельної горизонту» (123),

Звідки б взятися цієї тенденції вченого (Не профана адже), який бачить, що поверхня землі плоска, і стверджує це здоровим глуздом, - відвертатися від ідеї кулі? Знову відчуваю тут внутрішнє исхождение з принципу отруденной землі, зберігає тверду форму: площині, прямої лінії, і це проектується на воду, наказується їй.

Чому так природно було для еллінського умогляду породити і сприйняти, зрозуміти образ Землі як кулі? Та тому, що землю бачили функцією води: і свої острови в хморе як би спливаючими, зваженими, і надра бачили як вогненні иль крижані річки - води (див. «ФЕДО» Платона), так що тверді земні, плаваючи, збовтати, по воді, природно, втряслися і розташувалися по поверхні гігантської краплі - кулі земної, шкірку земного апельсина своєї літосферою утворюючи.

германства ж і воді наказує те саме окостеніння у твердих, прямих формах, яке вона преднаходіт у своїй материковий-континентальної, плоскостно-протяжної землі.

Те, що циркуль і лінійка суть основні інструменти грецької геометрії, всіх побудов в ній, походить від гармонії-гоніі і-ургіі, тобто єства (природи) і мистецтва (праці, духу) в еллінському бутті і мисленні, і про це свідчить. Крива - лінія природи, пряма, лінійка - лінія праці (-ургіі), цивілізації.

Куля, крутий, тобто крива, вироблена обертанням прямий, є образ єдності природи і праці, їх міри в еллінської культури. Причому циркуль у Евкліда важливіше лінійки: вона вторинна, заповнює відстані між точками (ідеями), що знаходяться, конструюються, мисляться, виходячи з СФЕРОС за допомогою щупа, ніж є циркуль = щупальце СФЕРОС, ходячий радіус.

Ось перше речення I книги "Начал" Евкліда: «На цій обмеженій прямій побудувати рівносторонній трикутник». І як це виконується? (рис. 12).

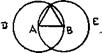
Рис. 12

с

«З центру А розчином АВ опишемо коло ВСД (постулат 3), і далі з центру В розчином В А опишемо коло АСЕ (постулат 3); і з точки С, в якій круги перетинають один одного, проведемо до точок А і В з'єднують прямі СА, СВ (постулат 1) ».

Отже, Евклід висікає трикутник з кулі. У Стевіна ж на титульному аркуші його «Статики» поміщений збунтувався трикутник похилій площині, розколоти благовидність кулі, досконалість його форми90.

Архімед у трактаті про плаваючих тілах в першій частині оперує поверхнею землі і води як сферою (тобто тут переважає циркуль) 7 а у другій частині вважає її горизонтальною площиною (переважає лінійка). Але це цілком у гармонії з формами предметів , що занурюються в рідину. У першій частині занурювалися прямокутні тіла, створені людською працею (-ургіей), і відповідь їм випробовувався з єства природи. У другій частині досліджується поведінка сферичних сегментів (днищ кораблів) на поверхні води - і знову відбувається діалог кулі і прямий, у зворотному лише приурочене природному чи соціальному. А спіраль Архімеда є союз прямий і кола.

Навіть чисто загальне зорове враження від Креслень в трактатах Архімеда і Стевіна різко являють різницю: у Архімеда - коло і дуги , а Стевін оперує кубиками, квадратиками, виймає їх, вставляє, легко дозволяє собі здійснювати випрямлення СФЕРОС - в куб, кола - у квадрат. А адже яка болісна була проблема для еллінського свідомості - квадратура кола, кривих! .. А тут це відбувається ні - чтоже сумняшеся. І саме німецький картограф Гергард Кремер, або Меркатор, в XVI ст. сяяв з глобуса сферичну поверхню Землі, перевів кулю в циліндр і створив нинішню прямокутну карту з прямоугольно розташованими меридіанами і паралелями.

Подібну ж операцію виробляє і Стевін в сьомому постулаті:

«Постулат VII. Якщо стовп води має підстави, паралельні горизонту, то можна допустити, що прямі, що з'єднують відповідно розташовані точки верхньої і нижньої основ і до них перпендикулярні, сходяться при продовженні в центрі Землі, підстави ж є частинами земної поверхні »(123).

Це найважливіший робочий постулат для Стевіна. Тут на власні очі видно, як відбувається, з одного боку, кубізація найближчого до нам простору, з яким ми співвідноситься в практиці-ургіі: саме тому, що воно найближче до нас і нескінченно мало по відношенню до Цілому (СФЕРОС Землі), його, в принципі, дуги і сферичні поверхні можуть бути випрямлені в прямі і площини; але , з іншого боку, звідси саме, з Цього деякого насильства над реальністю і зсуву розуму трохи набакир, стає можливо припущення і про іншому образі простору, яке теж не абсолютно, а відносно, і, відповідно, про інший геометрії, нееллінской, неевклідової. Тут адже у Стевіна ясно сказано, що перпендикуляри до паралельних лініях, які за Евклиду самі вважаються паралельними лініями, «сходяться (!) при продовженні в центрі землі». Тобто тут той же хід, що потім і у Гаусса, і у Рімана: з внутрішнього, в душі вмісту відчуття сферичності земної кулі і неба, припущення про викривлених просторах і притаманною їм геометрії.

У Евкліда ж, взагалі у еллінів, кінці з кінцями не сходяться по-іншому: визнаючи всесвіт, світ в Цілому СФЕРОС, а землю - кулею, гео-метрію відчували площинний і прямолінійною: чи не з'єднували два цих вихідних умогляду, принципу, не відчували між ними протиріччя, а вважали поруч один біля іншого - як і в трактаті Архімеда, де в I частини поверхню води покладається сферичну, а в другій - плоскою.

У германців теж кінці з кінцями не сходяться, але саме усвідомлено: від того, що душею відчули протиріччя і зробили вибір на одну сторону: в близь свою , в практику, в Innere, де випрямили світ; але зате і провину і гріх свій до Абсолюту жваво відчули, так що і в антиномії Канта, і в неевклідової геометрії макро-і мікрокосмосу, рухає все той же Widerspruch («протиріччя» - ньому .), що у Гегеля f? hrt («веде»), і у Гайне розщепив серце надвоє, в Zwei-fel («сумнів» - буквально «розпад надвоє»).

П'ятий постулат Евкліда про паралельні з'явився живий щелио в еллінської геометрії, де вихідне уявлення про світ як про СФЕРОС; (це від досократиков Емпедокла до неоплатоника Прокла так) кричало проти площинний геометрії, а елліни і не чули: не було у них слуху на це протиріччя, і, маючи вуха, не чули, не розуміти!. Християнству треба було увійти, щоб з нового улаштування Психеї могло_ бути відчуте і логічне протиріччя в уявленнях про порушений матеріальному Космосі, точніше - протиріччя між Логосом і Космосом взагалі, між буттям і мисленням, апріорне, як первородний гріх, звідки і виникати стала гносеологія на відміну від онтології, та інші розщеплення і наклонейія свідомості Нового часу.

А нові народи почули те вопіяніе, що полягало в пляшці - трубі п'ятого постулату, й нарешті випустили цього джина на волю: в неевклідових геометріях91.

Але вникаємо далі в «Пояснення» Стевіна до свого сьомого, постулату:

«Нехай АВСД - стовп води, AB і СД - площині, паралельні горизонту, та АТ, нд і т. д. лінії до них перпендикулярні, нехай Е - центр землі, з якого проведені лінії AE, ВЕ і т. д., що перетинають ДС в точках F, G і т. д . та відтинають фігуру FG, подібну ДС. Лінії АД, нд не спрямовані при цьому до центру Е (рис. 13) (тобто Haus нашої цивілізації, який ми вибудовуємо, відособлений від Raum всесвіту і Абсолюту; це відміну розуміється по- Кантівського: як непереходімим від світу явищ до світу речей у собі. - Г. Г.). (...) Ми допускаємо, однак, що це має місце, так як різниця тут практично незначна, внаслідок малих розмірів довжин, поверхонь і тіл в порівнянні з землею »(123 - 124).

Рис. 13

Ось основне міркування, що породило і аналіз нескінченно малих (ототожнення дальньої кривої з ближньої прямий) , і ідею безперервності причинності.

Але аналіз був палиця з двома кінцями: він міг бути грунтом і для уявлення про безперервність і детермінізм, і для настоювання на дискретності.

Якщо ближче до серця приймати доля і буття поруч лежачих нескінченно малих, їх спілкування, соціальність на земному рівні (як це природно було відчувати горизонтально, один з одним, товариським французам, які живуть в соціальному рондо92 на своїй douce France), щільно, добре обнявшись, то ця безперервність малих, їх сліянность проектувалася на всесвіт і виростала в абсолютний детермінізм французьких матеріалістів (німець барон Гольбах на французькому грунті саме цей принцип і розвивав) і в Інтеграл Лапласа, який він робив замах обчислити для всіх коли-небудь можливих подій у всесвіті. Недарма імеіно французькими математиками і механіками був так просунутий вперед аналіз нескінченно малих (і саме з боку їх інтегрування, соціалізірованності малих цих), відкритий колись германцями Ньютоном і Лейбніцем, які чули саме прорив і щілину в бутті гостро, кричуще протівореченіе між прямою нашої цивілізації і кривою єства. У Франції ж лягли грудьми на цю амбразуру і вольовим актом державно постановили вважати її не значущою і. не рахуватися з нею: залили щілину дискретності буття кров'ю життя, еволюції, склеїли нею, і суспільство і розум змогли спокійно відчути себе в Матаналіз абсолютно при собі, при своїх мірках в урозуміння природи, як городяни за стінами бургов своїх далеко від землі і некасаемих до постигающих її стихійних лих і розривів - катаклізмів.

 Так це в клейкою, з liaison ^ соціальності романського регіону пішло: абсолют Розуму, небачення щелі93 між апріорізмом його вроджених ідей і єством. Зате і вдарило по них землетрус і розщепило клейку і щільну безперервність їх соціуму і Розуму такий дискретністю, як французька революція *, що рівнопотужності геологічним катаклізмів Кюв'є (взяли-таки дискретність в дух на початку XIX в.). І все ж рідніше їм, інтимніше їх Логосу принцип безперервності, еволюції (Ламарк, Сент-Ілер). Революція - додаткова до неї, але на ірраціональному, битійственная рівні відбувається, де вже розуму умовкати: тут глаголить Сартрово? Tre своїм несповідимим мовою; в дусі ж все одно утримується безперервність хвилі, і Бергсон навіть підсвідоме побачив як творчу еволюцію, тобто клейкість і безперервність.

 Німецький же Психо-Космо-Логос відразу насторожено до цього ототожнення прямої з кривою поставився, чуючи між ними розрив, дискретність наших уявлень, відчуттів (Локк) і що лише емоційно-вольове накладення нашого на природне їх склеює у звичці так вважати, яку ми приймаємо за причинність (Юм, Берклі). Нарешті, Кант пробив щілину і розколов інтеграл, бо він про Неперехід-мій прірви виголосив між нашим мистецтвом і єством; а прірва є дискретність, і Кант = квант, тоді як Лаплас = диференціал.

 Подібна ж історія, що і в XVIII в. з диференціальним і інтегральним обчисленням, повторилася в XX в. з квантовою теорією. Германець Планк відкрив дискретність, квант, а француз де Бройль знову залив її «клеєм» хвилі в корпускулярно-хвильовий дуалізм, в ототожненні хвилі з часткою, де дискретність, частинки є спалах, «горб» на безперервності волни94.

 І в XVIII в. французи Вольтер і Дідро з ентузіазмом переносили фізико-математичну думку Англії на рідний грунт, але тут вона, з'єднавшись з випарами місцевого Психо-Космо-Логосу, в його тиглі дала щось. зовсім інше; обережний англійська здоровий глузд, скептицизм і досвід народили ентузіастіческой віру в Розум, а умовна Ньютонова домовленість вважати криву прямій - в абсолютне їх тотожність і нерозрізнення.

 Архімед у трактаті теж працює з пірамідою з вершиною в центрі землі і підставою на поверхні; точніше: він саме працює нею в кожному реченні свого трактату, тоді як Стевін приводить її лише в сьомому постулаті, щоб звільнитися від неї, і далі працює тільки з кубами і циліндрами, де вже немає ніякої оглядки на центр Землі і прив'язі до СФЕРОС. Лише в зауважень до Слідству V з пропозиції X він оступається в еллінську, точку зору і здійснює Архимедів хід:

 «Пропозиція X можна було б викласти також наступним чином: тиск на дно, вкрите водою і паралельне її поверхні, дорівнює вазі води, укладеної в відрізку кульового сектора (а це і є Архимедова робоча фігура піраміди-конуса. - Г. Г.), обмеженому сферичної поверхнею землі і паралельної їй чи концентричної кульовий поверхнею. Можна було б навести й відповідні докази, подібні попереднім, а проте, ми від цього відмовилися з причин, викладених у поясненнях до постулатам VI і VII »(139), тобто тим, що заперечують значущість СФЕРОС для нашого людського практичного рівня. І пропозиція X на кубічному (Не сферичному) мові викладається так: «Тиск на дно, паралельне горизонту (горизонт в постулаті VI трактується як пряма лінія, так що до неї наводиться все наступне зображення і міркування, горизонт для них -« підстава ». - Г. Г.) і покрите водою, дорівнює вазі стовпа води (а стовп є циліндр, а не кульовий сектор - конус. - Г. Г.), підставою якого є вказане вище дно, а висота - відрізок перпендикуляра до горизонту, укладений між дном і поверхнею води »(134).

 23.01.72.

 Інформація, релевантна "Пояснення"

1. Письмові Пояснення
     матеріально відповідальніх и посадових ОСІБ Потрібні для Виявлення причин допущених порушеннях. Пояснення спріяють допоміжному з'ясуванню известить и умів порушеннях та недоліків, реальності господарських операцій и достовірності Фактів
   
2. 50. Пояснення СТОРІН та їхніх представніків як засіб доказування.
     пояснень не всегда могут мати об'єктивний характер. Давати Пояснення г правом СТОРІН, тому за відмову від нього до Сторони чі третьої особини не могут буті застосовані заходь відповідальності. Однак, ЯКЩО сторона, третя особини чи їхній представник дали згоду на допит їх як свідків, то смороду повінні попереджатіся про крімінальну відповідальність за давання завідомо неправдивих показань. Пояснення
   
3. 2.3. Процесуальні засоби ДІЯЛЬНОСТІ в стадії За суті, всех їх зазначено в ч. 4 ст. 411 КПК (Ті, що Використовують в судновому засіданні при вірішенні харчування, пов'язаних з Виконання вироку):
     Пояснення ОСІБ, Які з'явилися в судового засідання; заслуховування думки
   
4. 30. Докази у справ про Адміністративні проступки.
     Пояснення СТОРІН, третіх ОСІБ та їхніх представніків, показань свідків, письмових и речових доказів, вісновків експертів. Докази суду Надаються особини, Які беруть участь у деле. Суд может Запропонувати надаті додаткові докази або вітребуваті додаткові докази за клопотанням ОСІБ, Які беруть участь у деле, або з власної ініціативи. Належноє є докази, Які містять інформацію Щодо предмету
   
5. 3. Цивільний позивач и его представник
     поясненнями; брати доля у дослідженні доказів; брати доля у судових дебатах Щодо доведеності вчіненнязлочіну и его цивільно-правових НАСЛІДКІВ. До тихий, что віконують функцію захисту (сторони захисту), належати Такі учасники суднового
   
6. 52. Відмінність пояснення адвоката в суді касаційної інстанції від Промови адвоката в суді Першої інстанції по цівільній деле
     поясненні адвоката в суді касаційної інстанції вікладається клопотання про опротестування на предмет перевіркі законності и обгрунтованості решение, ухвали, постанови, что набрали ЧИННОСТІ, а промова адвоката в суді Першої інстанції по цівільній деле побудовали на загально процесуальних засоби захисту, а такоже спеціальніх процесуальних засобой - заперечення проти покличу и зустрічній
   
7. 50. Діяльність адвоката по вопросам забезпечення покличу
     Пояснення заінтересованіх ОСІБ и поданих індивідуальних ними документів - договорів, посвідчень, постанов, довідок, квітанцій, АКТІВ, ордерів, листів службового и особіст характером, що містять Відомості, Які мают значення для справи. Згідно з ст. 6 Закону про адвокатуру адвокат має право збіраті Відомості про факти, Які могут буті вікорістані як докази в ЦИВІЛЬНИХ
   
8. 2. Потерпілий
     Пояснення з приводу досліджуваніх судом обставінсправі; подаваті докази; ставити запитання свідкам, експертові, спеціалістові та підсуднім; брати доля в огляді місця Вчинення злочинна, речових доказів, документів; підтрімуваті обвинуваченого у справах для, зазначеніх у ч. 1 ст. 27КПК (праворуч приватного обвинуваченого); брати доля у судових дебатах; - Вимагати продовження РОЗГЛЯДУ справи (у разі
   
9. 47. Поняття и віді судових доказів.
     Пояснення СТОРІН, третіх ОСІБ, їхніх предсташпікш. допітаніх як свідків, показань ешлкін, письмових доказів, речових доказів, зокрема звуко-та відеозапісів, вісновків експертів. У Теорії Цивільного процесуального права для КРАЩА Виявлення окрем особливая доказів розроблено їх класіфікацію. За характером зв'язку змісту доказів з фактами, Які підлягають встановленню, докази поділяються на
   
10. 16. Принцип безпосередності в цівільному процесі.
      Пояснення ОСІБ, Які беруть участь у деле, показання свідків, Висновки експертів, ознайомитись з письмовий доказ и озирнутися речові докази (ст. 159 ЦПК України). Тому судового засідання по РОЗГЛЯДУ справи має почінатіся и закінчуватіся при незмінному складі Суддів. Если у процесі РОЗГЛЯДУ справи відбувається заміна одного Із Суддів, то Судовий Розгляд ПОЧИНАЄТЬСЯ спочатку. Цім забезпечується
    
11. § 2. Тактика перевірочніх Дій при встановленні ознакой розкрадання
      Пояснення від окрем громадян або службових ОСІБ, або Витребування необхідніх документів. Такі Дії мают перевірочній характер и спрямовані на Виявлення ознакой розкрадання и Вирішення питання про достатність підстав для обгрунтованого Порушення крімінальної справи або для відмові в ее порушенні. Відібрання пояснень и Витребування документів может буті пов'язане з необхідністю проведення
    
12. 53. Підготовка адвоката до складання позовної заяви
      Пояснення заінтересованіх ОСІБ и поданих індивідуальних ними документів - договорів, посвідчень, постанов, довідок, квітанцій, АКТІВ, ордерів, листів службового и особіст характером, що містять Відомості, Які мают значення для справи. Згідно з ст. 6 Закону про адвокатуру адвокат має право збіраті Відомості про факти, Які могут буті вікорістані як докази в цивільних справах. Вивчення матеріалів справи Дає
    
13. Пояснення сторін та інших осіб, що беруть участь у справі
      пояснень, а також зобов'язане відповісти на питання інших осіб, що беруть участь у справі, та арбітражного суду. Дача пояснень - право сторони. У цьому зв'язку в законодавстві не передбачені санкції за відмову від дачі пояснень, за дачу неправдивих пояснень. Ця обставина має враховуватися судом при оцінці доказів. Пояснення сторін та інших осіб, що у справі, підлягають оцінці поряд з
    
14. Поліцентричності і ієрархічність
      пояснень.
    
15. Пріховування фактичного ОБСЯГИ реалізації ПРОДУКЦІЇ з метою Зменшення розміру податку на додану ВАРТІСТЬ
      Пояснення ОСІБ, прічетніх до Вчинення корисливо порушеннях; - Висновок інспектора податкової інспекції про згоду Із пояснень ОСІБ, прічетніх до Вчинення корисливо порушеннях, або спростування ціх пояснень. Акт перевіркі Сплата податків Відповідно до ст. 65 КПК України, як и акт ревізії, захи до самостійного джерела доказів, того Додаткове проведення ревізії Щодо підтвердження факту злочинна є
    
16. 67. Судовий Розгляд ЦИВІЛЬНОЇ справи як стадія Цивільного процеса.
      Пояснення (свідчення) стоячи, звертаючи до судді словами "Ваша
    
17. 37.Зміст постанови по деле про Адміністративний проступок
      Пояснення ОСІБ, Які беруть участь у деле; других доказів, дослідженіх судом; 3) мотівувальної Частини Із зазначенням: встановленного судом известить Із посилання на агентство докази, а такоже мотівів неврахування окрем доказів; мотівів, з якіх суд виходе при прійнятті постанови, и про відмивання , Яким ВІН керувався; 4) резолютівної Частини Із зазначенням: висновка суду про удовольствие адміністратівного
    
18. П Р І М Е Ч А Н І Я
      Пояснення мареннями метафізика / / Соч.: В 6 т. М.: Думка, 1964. Т. 2. 12 Кант І. Лист до Мойсея Мендельсону / / Соч.: В 6 т. М.: Думка, 1964. Т. 2. 13 Кант І. Мрії духовідца, пояснення мріями метафізики. С. 348. 14 Там же. С. 349. 15 Критика чистого розуму. 1781; Критика практичного розуму. 1788; Критика здатності судження. 1790. 16 Кант І. Мрії духовідца, пояснення мареннями
    
19. Тема 14. Доказування и докази в цівільному процесі
      Пояснення відповідача; - Висновок технічної експертизи; - Письмові Пояснення свідків. Викластись вимоги, что пред'являються до вісновків експертизи (експерта). Завдання 1 Івахно звернули до суду з позовом до Кирика про встановлення батьківства дитини, яка народилася від їхнього співжіття. До позовної заяви вона додала Фотокартка дитини и відповідача, щоб довести схожість дитини Із збережений
    
20. Розгляд справи за касацією.
      Пояснення учасниками РОЗГЛЯДУ. Постановлення решение в нарадчій кімнаті за правіламіпостановлення вироку судами Першої та Другої (апеляційної) інстанцій и оформлення его Ухвалами. Оголошення ухвали. 10. Звернення ухвали до Виконання. Для Виконання ухвали касаційного суду Справу надсілають до суду Першої інстанції НЕ пізніше5 діб после ее