
| Головна |
| «« | ЗМІСТ | »» |
|---|
Залежність концентрації беруть участь в реакції речовин від часу c (t) може бути отримана в аналітичному вигляді, якщо відомий вислів закону діючих мас для даної реакції. Відповідна тимчасова залежність називається рівнянням кінетики розглянутої реакції. Найбільш простий вид має рівняння кінетики реакції першого порядку.
Наприклад, експериментальне вивчення реакції гідролізу сахарози під дією соляної кислоти НС1 у водному розчині дозволяє представити отримані дані у вигляді рівняння

де з - концентрація сахарози, моль / л; до - константа швидкості.
Вираз (10.4) являє собою лінійне диференціальне рівняння першого порядку. Його інтегрування дає рівняння кінетики реакції першого порядку

Таким чином, залежність концентрації реагенту від часу описується в даному випадку показовою (експоненційної) функцією. Графік цієї функції є теоретичну кінетичну криву реакції першого порядку.
Дуже важливо для практичних застосувань, що теоретична залежність (10.5) дозволяє заздалегідь розрахувати концентрацію реагенту в будь-яке дослідника момент часу, якщо відома константа швидкості до і початкова концентрація зі. Отже, є можливість прогнозувати перебіг реакції в часі.
Експериментальні кінетичні криві також дають можливість прогнозувати перебіг реакції, але лише для вивчених початкових концентрацій і інтервалів часу. У цьому проявляється одна з переваг теоретичного опису. Крім того, теоретичне рівняння (10.5) підказує зручний спосіб обробки експериментальних даних для визначення порядку реакції і розрахунку константи швидкості.
Логаріфміруя вираз (10.5), отримують

або, після переходу до десятковим логарифмам,
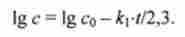
З виразу (10.6) випливає, що графік залежності логарифма концентрації реагенту Igc від часу t (Напівлогарифмічному координати) для реакції першого порядку є пряму лінію. Тангенс нахилу прямої дорівнює A: i / 2,3, звідки неважко розрахувати значення константи к. За аналогічною схемою знаходять рівняння кінетики реакції довільного порядку.
Нижче наведені експериментальні дані з вивчення швидкості осідання еритроцитів (ШОЕ):
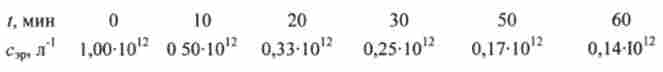
З цих даних випливає, що аглютинація (злипання) еритроцитів описується рівнянням кінетики другого порядку

де с, р - концентрація еритроцитів в плазмі, л '1; кг - константа швидкості.
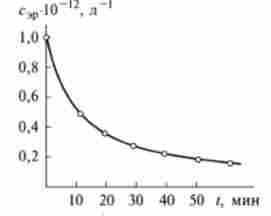
Мал. 10.3. кінетична крива осідання (реакція аглютинації) еритроцитів
На рис. 10.3 дані по кінетиці осідання еритроцитів представлені у вигляді кривої.
Вираз (10.7) являє собою лінійне диференціальне рівняння першого порядку другого ступеня за концентрацією Його інтегрування дає рівняння кінетики реакції другого порядку
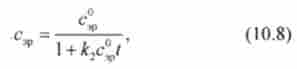
де з - початкова концентрація еритроцитів.
На основі теоретичного рівняння кінетики (10.8) отримують зручний спосіб графічної обробки експериментальних даних для реакції другого порядку. З цією метою рівняння (10.8) перетворять до вигляду

З виразу (10.9) випливає, що графік залежності зворотної концентрації реагенту 1 / с від часу / для реакції другого порядку - пряма лінія.
Для реакції аглютинації еритроцитів експериментальні точки графіка залежності 1 / с від часу / знаходяться на одній прямій, що узгоджується з законом другого порядку для ШОЕ. Константа швидкості кг = 10 13 (Л / хв) дорівнює тангенсу нахилу прямої.
Таким чином, залежність концентрації еритроцитів у плазмі від часу описується раціоназьной дробової функцією (рівняння гіперболи). Очевидно, що, як і в розглянутому вище прикладі, графік цієї функції є теоретичну кінетичну криву реакції другого порядку.
Реакція аглютинації еритроцитів являє собою окремий випадок кінетики другого порядку (рівняння (10.8)), коли початкові концентрації реагентів рівні.
У загальному випадку відповідно до закону діючих мас для швидкості (10.3) диференціальне рівняння, що описує реакцію другого порядку, має такий вигляд:

де сі сг - концентрації реагентів Хь Х2.
Як приклад можна привести реакцію взаємодії аніліну (реагент Х |) і оцтової кислоти (реагент Х2):
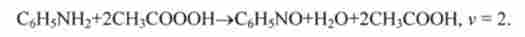
В результаті інтегрування отримують аналітичне рішення кінетичного рівняння (10.10):
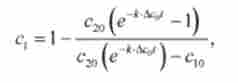
де Дс0 = з20 - з| 0 - різницю початкових концентрацій реагентів Х |, Х2.
Важливою кількісною характеристикою протікання реакцій у часі є час полупревращения t реагенту, яке визначається проміжком часу, протягом якого початкова кількість реагенту «про або його початкова концентрація З зменшуються в ході реакції вдвічі.
Якщо рівняння кінетики реакції відомо, час полупревращения неважко виразити через константу швидкості. Для цього в рівняння кінетики підставляють значення / = / | / 2 і з = У2. В результаті з рівняння кінетики реакції першого порядку (10.5) отримують час полупревращения, рівне

З рівняння кінетики реакції другого порядку (10.8) відповідно отримують

У метаболічних перетвореннях, як правило, беруть участь кілька реагентів: субстрати, ферменти, коферменти, кофактор. Не завжди відомі всі беруть участь в реакції речовини, тому за ходом перетворення стежать за зміни кількості або концентрації одного, рідше двох реагентів або продуктів. У таких випадках вираз швидкості через концентрацію невідомо і час полупревращения використовують як зручну кінетичну характеристику досліджуваного речовини. Але при цьому необхідно мати на увазі, що на відміну від константи швидкості ця кінетична характеристика може залежати від початкової концентрації речовини.
Цей факт наочно демонструється виразом для часу полупревращения реакції другого порядку (10.12). В цьому випадку час полупревращения залежить не тільки від константи швидкості, але також і від концентрації реагенту.