Фігури і модуси простого категоричного силогізму
- Залежно від того, яке місце - суб'єкта або предиката - в посилках займає середній термін, розрізняють чотири різновиди силогізму, звані фігурами простого категоричного силогізму. Кожна фігура має свої спеціальні правила, хоча ці правила можуть бути отримані строго логічно, як наслідку із загальних правил простого категоричного силогізму.
I. Перша фігура характеризується тим, що середній термін (М) грає в ній роль суб'єкта в більшому і предиката у меншому посилці. Перша фігура простого категоричного силогізму використовується в процесі пізнання як спосіб поширення деякого загального знання, вираженого в більшій посилці, на деякі особливі випадки - клас предметів виражаються меншим терміном (S). У зв'язку з цим дану фігуру характеризують як спосіб підведення класу S під клас М, щодо якого є загальне знання.
Правила першої фігури:
Велика посилка - загальне судження.
Менша посилка - стверджувальне судження.
II. Друга фігура характеризується тим, що середній термін (М) грає роль предиката в обох посилках. Дана фігура використовується в основному як засіб спростування деяких неправильних підведень чого-небудь під деяке поняття. Правила другої фігури:
Одна з посилок повинна бути негативним судженням.
III. У третій фігурі середній термін (М) грає роль суб'єкта в обох посилках. В основному третя фігура може застосовуватися в якості способу спростування необгрунтованих узагальнень. Правила третьої фігури:
Менша посилка повинна бути ствердною суж-дением.
Висновок - приватне судження.
IV. У четвертій фігурі середній термін (М) є предикатом більшою і суб'єктом в меншій посилці. Дана фігура являє собою штучне побудова і не має ніяких певних пізнавальних функцій.
Правила четвертої фігури:
Якщо одна з посилок - негативне, то велика посилка - загальне судження.
Якщо велика посилка - стверджувальне судження, то менша - загальне судження.
Якщо менша посилка - стверджувальне судження, то висновок - приватне судження.
Всі чотири фігури простого категоричного силогізму можна представити у вигляді графічних схем:
I
II
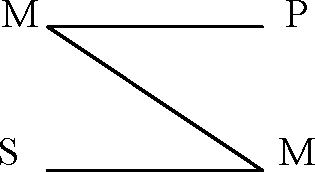
S - Р
Р
м
S
м
S - Р
IV

м
p
p
M
M
s
M
s
Ill
S - P
- Модус - це різновиди силогізму всередині кожної фігури, що розрізняються характером суджень, - посилок і висновку, - складових силогізм. Враховуючи наявність чотирьох типів категоричних суджень - общеутвердітельних (А), общеотріцательних (Е), частноутвердітельних (I) і частноотріцатель-них (О) - можна підрахувати, що в кожній фігурі є 64, а всього (для всіх чотирьох фігур) - 256 модусів . Однак не всі вони являють собою правильні умовиводи. Таких - правильних модусів - всього лише 24, тобто по 6 модусів в кожній фігурі. Серед них виокрем-ляется 19 основних або так званих сильних модусів, які повністю задовольняють загальним правшам простого категоричного силогізму і спеціальним правшам фігур. Решта - сла-які модуси - можуть бути представлені як складні висновки: поєднання висновків у формі категоричного сшлогізма з висновками по правшам «логічного квадрата».
Інформація, релевантна " Фігури і модуси простого категоричного силогізму "
- 5.3. Індуктивні умовиводи І умовиводи ПО аналогії
фігури і модуси силогізму? Які особливі правила мають 1-а, 2-а і 3-тя фігури? Охарактеризуйте значення цих фігур в пізнанні. Чим неповна індукція відрізняється від повної? Список літератури Бочаров В.А., Маркін В.І. Основи логіки. М., 1998. Горський Д.П., Івін А.А., Никифоров А.Л. Короткий словник по логіці. М., 1991. Івін А.А. Логіка. М., 2000. Івлєв Ю.В. Логіка. М., 1998. Кирилов В.І., Старченко - ЕКЗАМЕНАЦІЙНІ ПИТАННЯ
модуси категоричного силогізму. Умовний і умовно-категоричний силогізм. Способи перевірки правильності модусів. Розділовий і розділової-категоричний силогізм. Умовно-розділовий силогізм. Дилема. Складні, скорочені і складноскорочені силогізми: полісіллогізм, ентимема, смітить і Епіхейрема. Види індукції. Співвідношення індукції та дедукції. Індуктивні методи встановлення - 5.2. Дедуктивні умовиводи
фігурами силогізму. У посилках простого категоричного силогізму середній термін може займати місце суб'єкта або предиката. У першій фігурі середній термін займає місце суб'єкта в більшому і місце предиката у меншому посилці. Правила 1-й фігури. Велика посилка - загальне судження. Менша посилка - стверджувальне судження. 1-я фігура - найбільш типова форма дедуктивного умовиводи. Усі - Скорочений силогізм - ентимема
фігура силогізму і порядок посилок. Форму ентимеми можуть також брати умовно-категоричний силогізм, розділової-категоричний, умовно-поділу-лительного - контрольні роботи
простих суджень. Категоричні судження та їх види. Розподіленість термінів у категоричних судженнях. У даній темі важливо визначити судження як форму мислення, перш за все з точки зору його істинності чи хибності. Також необхідно з'ясувати, що об'єднує і в чому відмінності між судженням і пропозицією. Потрібно звернути увагу, перш за все, на структуру судження. Вивчення суджень - питання До іспиту ПО логіці
категоричний силогізм. Індуктивні умовиводи. Поняття індукції. Повна індукція. Неповна індукція. Популярна індукція. Наукова індукція. Аналогія. Поняття аналогії. Види аналогії. Логічні основи аргументації. Аргументація. Доказ. Способи аргументації: обгрунтування і критика. Правила і помилки в аргументації. Контрольні питання. Гіпотеза. Поняття і види гіпотез. Побудова - 3.3. Опосередковані умовиводи. Простий категоричний силогізм
простого категоричного силогізму Категоричний силогізм - це таке опосередковане дедуктивний умовивід, посилками і укладанням якого є категоричні судження. Наприклад: Всі риби дихають зябрами Карась - риба Карась дихає зябрами Поняття, що є суб'єктом укладення, називається меншим терміном і позначається символічно «S». У наведеному вище прикладі йому відповідає - Загальні правила простого категоричного силогізму
простого категоричного силогізму. У даному випадку необхідність кожного правила означає, що якщо воно не виконується в деякому умовиводі, то умовивід неправильно. Достатність же всіх загальних правил виражається в тому, що виконання кожного з них свідчить про правильність умозак-люченія. Іншими словами, силогізм правильний, якщо виконані всі правила простого категоричного - Правша термінів
простому категоричному силогізмі має бути три терміна. Порушення цього правила веде до помилки, званої «учетверение терміна». Вона відбувається через порушення закону тотожності, коли один і той же термін використовується в різних сенсах. Наприклад: Рух - вічно Ходіння в університет - це рух Ходіння в університет - вічно Середній термін повинен бути розподілений хоча би в одній з - 3.4. Скорочені, складні і складноскорочені силогізми
простим категоричним силогізмів існують різні види складних силогізмів. Серед них: полісіллогізм - складні силогізми, що представляють собою такі послідовності певним чином пов'язаних між собою простих категоричних силогізмів, що укладення попереднього служить посилкою наступного. Існують також і складно-скорочені силогізми - смітить і Епіхейрема - результати