2.4. Відносини між судженнями по істинності. Логічний квадрат
Подпротівние Q
Відносини між судженнями поділяються на сумісні і несумісні. Оскільки найважливішою характеристикою судження є його властивість бути або істинним, або хибним, то між судженнями різної кількості і якості, але мають один і той же суб'єкт і предикат, можна виділити наступні відносини по істинності: ставлення протиріччя чи контрадікторності; ставлення протилежності або контрарності; ставлення подпротів-ності; відношення підпорядкування. Сумісними є відносини підпорядкування і подпротівності. Несумісними є відносини протилежності (контрарності) і протиріччя (контрадікторності). Несумісні судження не можуть бути одночасно істинними, але можуть бути одночасно хибними.
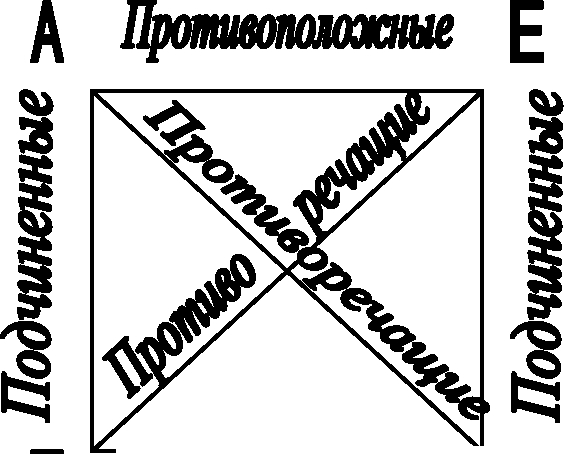
Ці відносини прийнято зображати у вигляді схеми - так званого «логічного квадрата». Букви «А», «Е», «I», «О», поміщені в кутах квадрата, позначають види суджень, а сторони і діагоналі - можливі відносини між судженнями.
Відносини протиріччя (А - О; Е - I) між судженнями з однаковими суб'єктами і предикатами характеризуються тим, що
знаходяться в цьому відношенні судження не можуть бути одночасно ні істинними, ні хибними. Якщо одне з суперечать суджень істинно, то інше з необхідністю помилково і навпаки - якщо одне з них помилково, то інше істинно. Прикладом суперечать висловлювань є наступні: А - «Всі люди смертні» і О - «Деякі люди не є смертними»; Е - «Жоден пацифіст не хоче війни» і I - «Деякі пацифісти хочуть війни». Символічно відношення протиріччя записуються так:
А ^ д. Vx (S (x) => P (x)) => 3x (S (x) aP (x))
А ^ О: Vx (S (x) з Р (х)) з 3x (S (x) л P (xj)
Якщо не вірно, що всі S суть Р, то вірно, що деякі S не суть Р.
0 => Л: Ех (я (х) ЛР (х)) з Vx (s (x) => Р (х))
Якщо вірно, що деякі S не суть Р, то невірно, що всі S суть Р.
д ^ А: Ех (я (х) ЛР (х)) з Vx (s (x) => Р (х))
Якщо невірно, що хоча б деякі S не суть Р, то вірно, що всі S суть Р.
? З7: Vx (S (x) з Р (х)) з 3 X (S (X) Л P (x))
Якщо вірно, що жодне S не суть Р, то невірно, що деякі S суть Р.
Е з /: \ / x (S (x) з P (xj) з 3x (S (x) л Р (х))
Якщо невірно, що жодне S не суть Р, то вірно, що деякі S суть Р.
Якщо вірно, що деякі S суть Р, то невірно, що жодне S не суть Р.
7З?: Зх (^ (х) ЛР (ї)) зVx (s (x) ЗР (х))
Якщо невірно, що хоча б деякі S суть Р, то вірно, що жодне S не суть Р.
Ставлення протилежності (А - Е) характеризується тим, що знаходяться в цьому відношенні судження не можуть бути одночасно істинними, але можуть бути одночасно хибними. Звідси випливає, що якщо одне з протилежних суджень істинне, то інше помилково, але не навпаки, тобто, якщо одне з них лож -но, то інше невизначено. Приклади протилежних висловлювань. А - «Всі риби дихають зябрами» - істинно, Е - «Жодна риба не дихає зябрами» - помилково. Символічно відношення протилежності записується так:
А з Е: Vx (S (x) з Р (х)) з Vx (s (x) з P (x) j
Якщо вірно, що всі S суть Р, то невірно, що жодне S не суть Р.? З2: VX (S (X) DP (I)) ЗVX (S (X) DP (X))
Якщо вірно, що жодне S не суть Р, то невірно, що всі S суть Р.
Ставлення подпротівності (I - О) характеризується тим, що судження, що знаходяться в цьому відношенні, не можуть бути одночасно хибними, але можуть бути одночасно істинними . Звідси випливає, що якщо одне з них помилково, то інше істинно. Якщо ж одне істинно, то інше невизначено. Наприклад: О - «Деякі люди бували на Марсі» - помилково, I - «Деякі люди не бували на Марсі» - істинно . Символічно це відношення записується так:
Якщо невірно, що деякі S суть Р, то вірно, що деякі S не суть Р.
Od /: Зх (Я (Х) ЛР (Х)) зЗХ (? (Х) ЛР (Х))
Якщо невірно, що деякі S не суть Р, то вірно, що деякі S суть Р.
Ставлення підпорядкування (А - I; Е - О) характеризується тим, що істинність підкоряють (загальних) суджень (А; Е) обумовлює істинність підлеглих (I; О), але не навпаки. Водночас хибність підлеглих (приватних) суджень (I; О) обумовлює хибність підкоряють (А ; Е), але не навпаки. Наприклад, з істинності общеутеердітельного судження (А) «Все планети світять відбитим світлом» слід істинність частноутеердітельного судження (I) «Деякі планети світять відбитим світлом». символічний це відношення записується так:
А => 1: V (x) (S (x) => Р (х)) з 3 (х) (^ (х) ЛР (х)).
Якщо вірно, що всі S суть Р, то вірно, що деякі S суть Р.? DO: Vx (S (X) DP (I)) ЗЗХ ^ (Х) ЛР (Х))
Якщо вірно, що жодне S не суть Р, то вірно, що деякі S не суть Р.
7Зa: 3 (x) (s (x) ap (x)) = > v (x) (s (x) => p (x))
Якщо невірно, що деякі S суть Р, то невірно і те, що всі S суть Р.
Оз?: 3x (S (x) ЛР (Ї)) з Vx (S (x) DP (X))
Якщо невірно, що деякі S не суть Р, то невірно і те, що жодне S не суть Р.
Інформація, релевантна "2.4. Відносини між судженнями по істинності. Логічний квадрат"
- ЕКЗАМЕНАЦІЙНІ ПИТАННЯ
відношення між ними. Види понять . Поняття роду та виду. Операції обмеження й узагальнення понять. Відносини між поняттями. Операції над класами: об'єднання (додавання), перетин (множення), віднімання (різницю), додаток (заперечення), поділ (зворотне множення). Нульовий і універсальний класи , їх властивості і відносини між ними. Закони логіки класів. Поділ понять. Види і правила - 4.2. Прості судження
відношення між предметами або факт існування предмета, - вони діляться на атрибутивні, судження з відносинами, екзистенційні. Судження, в яких ознака предмета приписується (або заперечується) предмету, називаються атрибутивними судженнями (судження властивості). Наприклад: «Ніхто із суддів не має права утримуватися від голосування». судженнях з відносинами. У цих судженнях йдеться про - 5.2. Дедуктивні умовиводи
відносин контрадікторності: Аі ^ 0л; Ал ^ 0і; 0і ^ Ал; 0л ^ Аі; Еи ^ Іл; Їв ^ іи; іи ^ Їв; Іл ^ Єї. Наприклад: Якщо судження «Всі кити - ссавці» (А) істинне, то судження «Всі кити - НЕ ссавці» (О) буде хибним (Аі ^ 0л). Висновки з відносин контрарності: Аі ^ Їв; Ал ^ Е?; Еи ^ Ал; Їв ^ А? Висновки з відносин субконтрарности: Іл ^ 0і; іи ^ 0?; 0л ^ іи; 0і ^ І? Висновки з відносин підпорядкування: Аі ^ 1и; Еи ^ Оі; 1та ^ А?; - 5.3. Індуктивні умовиводи І умовиводи ПО аналогії
відносин. Аналогія предметів - умовивід, в якому об'єктом уподібнення виступають два одиничних предмети, події або явища, а стерпним ознакою - властивості цих предметів. Аналогія відносин - умовивід, в якому об'єктом уподібнення виступають відносини між двома парами предметів, а стерпним ознакою - властивості цих відносин. За іншим критерієм аналогію можна розділити на - контрольні роботи
відносини між поняттями і покажіть його з допомогою кругових схем: Чиновник, державний службовець, російська, громадянин. Учасник Великої Вітчизняної війни, генерал, ветеран, полковник. Дипломат, посол, консул, розвідник . Вправа 3. Встановіть вид складного судження: з'єднувальні (кон'юнктівние), розділові (строга або нестрога диз'юнкція), умовні (імплікатівние) або - Умовивід по логічному квадрату
відносини між категоричними судженнями А, Е, I, О, які зображуються за допомогою «логічного квадрата», можна будувати висновки, грунтуючись на істинність або хибність вихідного судження. Висновки будуються за такими правилами: Відносини протиріччя (А-О; EI); А з О; А з О; Е з!; І з І; О з А; О з А; І з I;! з Є. Ставлення протилежності або контрарності (А-Е): А з Е; Е з А; (4 => (? vl); - 1. Поняття і класифікація доказів. Предмет доказування
відносини, пов'язані з судовим доведенням, то може скластися враження, що в арбітражному процесуальному законодавстві знайшла вираження концепція судового доказування як засоби переконання суду, оскільки термін «доведення» застосовується тільки щодо діяльності сторін, але не суду, наприклад, кожна сторона повинна довести ті обставини, на які вона посилається як на - 21. Романо-германська, англосаксонська, мусульманська правова сім'я
відносин. Англосаксонська правова сім'я - Англія, США, Нова Зеландія, Канада, Австралія, Індія. В Англії, в період нормандського завоювання, існувало розрізнене, не пов'язане між собою локальне нормотворчість, засноване на місцевих звичаях. Починаючи з 10 в., королівські судді починають формування єдиного для всієї країни права. Прийнято рішення приймаються за основу всіма іншими суддями, - ВСТУП
стосунки. Держава, забороняючи під страхом кримінального покарання вчинення зазначених діянь, ставить своєю заду-1 Див Ф. Енгельс. Анти-Дюрінг, 1966, стор 112. чий впливати на поведінку людей в напрямку, відповідному інтересам суспільства. При цьому обгрунтування кримінальної відповідальності, в якій концентрується пізнавальна та оціночна діяльність органів, які відправляють - § 4. Теорії складу злочину як єдиної підстави кримінальної відповідальності
відносно складу злочину і приготування, замаху і співучасті, для вирішення цієї проблеми пропонує «уточнити визначення складу злочину, що дається в радянській 1 В. Н. Кудрявцев. Теоретичні основи кваліфікації злочинів. М., 1963, стор 76. Водночас В. Н. Кудрявцев допускає, на нашу думку, неточне тлумачення ролі діспоз ції в конструюванні поняття складу