1.1. Потенційна реальність
Основу викладається в цій книзі теорії еволюції утворює поняття потенційної реальності, або потенційності, що взаємодіє з актуалізоваяним світом.
Потенційним зазвичай називають можливість, що створює умови для виникнення акуталізована (локалізованих в про странстве і часу і взаємодіючих між собою) об'єктів, подій і процесів. Однак таке розуміння потенційності недостатньо, оскільки воно залишає в тіні притаманну потенційності двоїстість. З одного боку, це можливість існування акуталізована об'єктів. З іншого боку, це можливе існування, тобто особливий вид реальності, що дозволяє говорити не просто про можливість, а про потенційний бутті або про потенційну реальності.
Щоб надати цим абстрактних міркувань більш конкретний зміст, зв'яжемо відмінність між актуальним і потенційним існуванням з добре відомим в науці відмінністю між стійким і нестійким існуванням. Нагадаємо їх визначення.
Нехай X (?) - Поточний стан системи, - її стаціонарний стан і X (Ь) знаходиться в деякій околиці Хв. Стан Х% локально стійко, якщо існує порогове значення 7] таке, що будь-яке обурення? ^ 7) ОСТаВЛЯСТ X (1) у зазначеній околиці. Якщо Х (1) залишається в цій околиці за будь-яких збурюваннях, то X, глобально стійко. Наприклад, термодинамічна рівновага ізольованої системи глобально стійко.
Поняття стійкості і нестійкості традиційно застосовуються по відношенню до стаціонарним станам системи, тобто станам, формальний опис яких не залежить від часу і які можуть існувати «досить довго». Стаціонарне стан стійко, якщо при невеликому відхиленні від нього система повертається в цей стан, і нестійко, якщо відхилення від нього ростуть з плином часу. Крім стійкості і нестійкості стаціонарних станів можна говорити про структурну стійкість і нестійкості системи. Математичні моделі систем, обла-дають цим властивістю, стали називатися «грубими» (їх структура не змінюється при малих впливах на систему).
Довгий час передбачалося, що тільки структурно стійкі системи існують «насправді», оскільки структурно нестійкі системи швидко руйнуються неусувними малими впливами. Відомо, однак, що за певних умов нестійкий стан знову може придбати стійкість і існувати в звичайному сенсі (подібно до того як одного разу вилікувана хвороба - може повернутися до людини знову). Це і дозволяє говорити про потенційності як про реальність, яка об'єднує існування всіх нестійких об'єктів і процесів. Потенційність - це вмістилище всіх нестійкостей.
З позицій акуталізована реальності нестійкийоб'єкт зникає. З позицій потенційної реальності нестійкийоб'єкт продовжує існувати. Це змушує нас повернутися до позиції еліатів, які стверджували, що небуття немає і бути не може, так як затвердження «небуття є» є логічним суперечністю і тому неможливо. Для примирення цього здавався екстравагантним затвердження з реалістично налаштованими опонентами, які своїми очима бачать зникнення тих чи інших речей і довіряють своїм відчуттям, достатньо припустити, що небуття в звичайному сенсі означає буття в деякому іншому світі, недоступному прямому сприйняттю. Саме це і запропонував зробити Платон. Однак недоступність прямому сприйняттю не є найважливішою рисою цього іншого світу. Більш істотна його зв'язок з сприймаються світом.
Доступна прямому сприйняттю акуталізована реальність характеризується взаємодіями локалізованих у просторі та часі об'єктів і процесів, що задовольняють принципу причинності в тій чи іншій його формулюванні. До сьогоднішнього дню'она вивчена відносно непогано, оскільки донедавна акуталізована реальність була єдиним об'єктом наукового інтересу.
Сучасна наука, однак, все частіше стикається з незвичним доя «реаліста» поведінкою акуталізована об'єктів. Прикладом може служити фізичний феномен нелокал'ності, що виникає в ЕПР-експериментах. Як відомо, при зіткненні позитрона і електрона народжується пара фотонів, які розлітаються зі швидкістю світла і тому не взаємодіють між собою. Виміряємо імпульс одного із них, не вимірюючи імпульсу іншого. Тоді, в силу закону збереження імпульсу, можна правильно передбачити величину імпульсу другого фотона до його вимірювання. Тому, якщо квантова механіка справедлива, то необхідно припустити, що вимірювання імпульсу одного з фотонів впливає на фізичний стан іншого,
незважаючи на те, що в звичайному сенсі вони не взаємодіють. Як це пояснити?
Існують різні відповіді на це питання: а) фотони взаємодіють «миттєво», з нескінченно великою швидкістю, б) вони взаємодіють з порушенням принципу причинності; в) взаємодія між ними носить інформаційний характер, причому інформація поширюється з надсвітовою швидкістю; г) ніякої взаємодії взагалі не відбувається. До виміру обидва фотона потенційно існують як єдиний цілісний об'єкт, тому неможливо впливати на один із них, не впливаючи тим самим на «інший». Останній з цих відповідей неявно і незалежно від того, усвідомлюємо ми це чи ні, вводить поняття потенційної реальності.
Будучи теоретичною конструкцією, поняття потенційної реальності, щоб бути ефективним, має задовольняти певним умовам. По-перше, воно має володіти значною пояснюватиме силою: пояснювати такі результати експериментів, спостережень і накопиченого соціального досвіду, які важко або неможливо пояснити інакше. По-друге, воно має задовольняти умові непрямої наблюдаемості, обумовленою тим, що сама потенційна реальність повинна надавати спостережуване вплив на емпірично сприймається людиною акуталізована світ. По-третє, потенційна реальність повинна володіти непустою набором характеристичних властивостей. Обговоримо ці властивості.
Насамперед, це властивість цілісності (неможливості виділення в ній окремих локалізованих об'єктів). До розуміння цілісності найпростіше прийти, зіставляючи цілісність і ціле. Ціле - це сукупність взаємодіючих частин, в якій сенс поняття «частина» визначається властивим системі взаємодією. Взаємодії відносяться до акуталізована реальності і тому спостережувані. До них застосовні поняття не тільки частини і цілого, але також простору, часу, причини, еволюції і т.д.
Системи, що володіють властивістю цілісності, навпаки, не мають явно виражених частин і взаємодій. Подібно квантовим об'єктам до спостереження (до взаємодії з приладом), вони не мають ні просторово-часових, ні причинних характеристик, а застосування до них понять взаємодії, частини і цілого непродуктивно: будь-яка частина виявляється рівної цілому, а всі взаємодії реалізується миттєво (з « нескінченно великою »швидкістю). Функціонально властивості цілісності відповідає нелокал'ност', або такий вплив однієї «частини» цієї системи на іншу, яке не можна пояснити взаємодією між ними (див. Костюк, 1989).
Поняттю цілісності в зазначеному сенсі близько поняття Єдиного, введеного Платоном. На його думку, єдиним не можна без протиріччя приписати ніяких інших властивостей, крім властивості «бути єдиним».
Таке єдине неподільне (не має частин) і не може існувати актуально, утворюючи, однак, передумову акгуалізованного існування. «Якщо єдиного не існує, то нічого не існує» [Платон. Парменід, 166в-с].
Феномен цілісності можна охарактеризувати також за допомогою поняття симетрії (ця ідея знову сходить до Платона). «Симетрія позначає той вид узгодженості окремих частин, який об'єднує їх в єдине ціле» [Вейль, 1952, с. 35]. Перестановка «чистий» в симетричних перетвореннях нічого не змінює, і нові стану системи виявляються не відрізнятись від старих. Тому цілісність, яка не має частин, володіє найбільшою симетрією. Асиметрія, навпаки, розділяє цілісність на окремі частини, або підсистеми. Перехід від цілісності до цілого може бути зрозумілий тому як порушення максимальної симетрії, властивої цілісності. При цьому порушення даної симетрії призводить до появи інший, менш загальної, але більш складної симетрії.
Другим найважливішим властивістю потенційної реальності є її прихована (неявна) альтернативність. Введення цієї властивості в науковий ужиток пов'язане з ім'ям Арістотеля. Він звернув увагу на те, що відсутність в потенційності акуталізована частин не перешкоджає наявності в ній потенційних альтернатив, які з точки зору актуального буття несумісні між собою. «У можливості одне і те ж може бути разом [обома] протилежностями, але насправді немає» (Арістотель, Метафізика, Г, 1009с, 35). Наприклад, хоча здоров'я протилежно хвороби, але тіло містить можливість і того, й іншого. Потенційна альтернатива не є «частиною», але може стати такою в процесі її реалізації.
Наявність прихованих альтернатив у потенційній реальності ставить питання про способи їх реалізації. На якій підставі відбувається актуалізація однієї з альтернатив? Чому, скажімо, акуталізована А, а не не-а (або, навпаки, акуталізована не-а, а не А)?
На думку Лейбніца, який вивчав цю проблему (див. Лейбніц, 1680, 1685), з двох альтернатив А і не-4 реалізується та, яка досконаліша або вірогідніша. Однак у цьому рішенні містяться приховані труднощі, оскільки не виключено, що при такому аналізі проблеми ми міняємо місцями причину і наслідок. Може виявитися, що щось актуалізації не тому, що воно більш імовірно, навпаки, воно більш ймовірно тому, що актуалізуються. І тоді механізм актуалізації залишається незрозумілим.
Проте, ідея Лейбніца є, швидше за все, правильної, досить замінити поняття ймовірності поняттям малих випадкових збурень (флуктуацій). Останні, як ми знаємо, відіграють фундаментальну роль у визначенні стійкості і нестійкості я тим самим у поділі буття на акуталізована і потенційну реальність. Малі флуктуації видаляють нестійкийоб'єкт з ак-туалізованного світу і зберігають його в потенційній реальності в нелокалізованого вигляді. Це передбачає наявність у потенційній реальності деякого аналога хвильової функції в квантовій механіці. Така функція не повинна залежати від часу в силу відсутності такого в потенційної реальності.
Малі випадкові збурення утворюють, таким чином, якийсь «природний фон» потенційної реальності. Їх різке посилення, навпаки, може призвести до актуалізації деякої потенційної альтернативи. При цьому в рамках потенційної реальності некоректно ставити питання про причини різкого посилення флуктуацій (через відсутність причинності у потенційній реальності). Замість цього можна говорити про спонтанне (мимовільному) посиленні флуктуацій і, відповідно, про спонтанної актуалізації тієї чи іншої неявній альтернативи.
Крім того, не слід думати, що потенційна реальність існує сама по собі, на зразок світу ідей Платона. Насправді це ідеалізація, яка корисна як часткове (додаткове) опис реальності як такої, іншої додаткової характеристикою якої є акуталізована реальність. Реальність як така, або Буття - це постійно мінлива «суміш» актуальною і потенційної складових, що взаємодіють між собою. Посилення флуктуацій можна вважати одним з можливих результатів такої взаємодії.
Якщо таке розуміння механізму посилення флуктуацій є правильним, то його результат можна зрозуміти як «обмін стійкістю»: потенційна альтернатива набуває стійкість і актуалізації, а бере участь в обміні актуальний об'єкт втрачає стійкість, справа-Калізія і стає однією з незліченних прихованих альтернатив у потенційній реальності1}.
1 (Термін «обмін стійкістю» ввів, наскільки відомо автору, В. І. Арнольд (Арнольд, 1989).
Представлення про потенційну реальності дозволяє пояснити і фундаментальне відмінність між строгим детермінізмом хвильової функції в рівнянні Шредінгера і випадковим розподілом результатів її вимірювання. «Елемент непередбачуваності та випадковості виникає лише при спробах інтерпретації хвилі на основі уявлень про становище і швидкості частинок. Але в цьому-то, можливо, і полягає наша помилка: може бути, немає ні положень, ні швидкостей частинок, а існують одні тільки хвилі »(Хокінг, 1988, с. 145). Однак замість хвиль, що піднімають стару суперечку про відносні переваги хвиль і частинок при описі фізичної реальності, краще говорити про потенційну реальності, що не містить в явному вигляді ні хвиль, ні частинок, але здатної при актуалізації породити або те, або інше, або щось третє.
Таким чином, характеристичними властивостями потенційної реальності є властивості цілісності, прихованої альтернативності, наявність неусувного фону малих випадкових збурень (флуктуацій), а також існування механізму обміну стійкістю (нестійкістю). При цьому цілісність є основоположним властивістю потенційної реальності, зумовлюючи в чому інші її характеристики.
Використовуючи концепцію потенційної реальності, можна пояснювати квантовомеханічні ефекти. Так, квантовомеханічний принцип невизначеності може бути пояснений тим, що при актуалізації (зокрема, при вимірі) зберігаються «сліди» вихідної потенційності. Аналогічно можна пояснити наявність властивостей у «порожнього» простору, яке насправді «заповнене» потенційністю, приймаючої вид флуктуацій. Концепція потенційної реальності дозволяє пояснювати також багато складні й тонкі ефекти еволюційних процесів у соціально-економічній сфері. Вся наша книга - спроба рухатися в цьому напрямку.
Нелінійність, критичність, нерівновага. Потенційна реальність впливає не тільки на акуталізована світ в цілому, але і на окремі об'єкти цього світу. Для характеристики цього впливу ми використовуємо поняття простого і складного об'єктів.
Назвемо об'єкт складним, якщо він має як актуальну, так і потенційну складову. Об'єкти, що не мають потенційної складової, назвемо простими. Потенційна складова пов'язує складний об'єкт з буттям загалом, тому поведінка складних об'єктів може виявитися несподіваним і неоднозначним з точки зору їх локального (акуталізована) існування.
Введення складних об'єктів має вирішальне значення для подальшого викладу. Вони дозволяють говорити про єдиний з позицій багато чого, про цілісність - з позицій взаємодії локалізованих частин, про філософську абстракції - з позицій конкретних моделей, що використовуються в сучасній науці. Складні об'єкти, що мають дворівневу структуру (вони одночасно належать і Єдиного, і Багато чому) дозволяють обійти труднощі, зазначену Платоном: Єдине може мати тільки властивість «бути Єдиним», в іншому випадку (тобто якщо воно володіє і іншими властивостями) воно вже не жодної, а Багато чого.
На рівні наукових теорій відмінність між простими і складними об'єктами проявляється як відмінність між лінійними і нелінійними моделями. Розглянемо приклад лінійної системи *. Два однакових посудини з'єднані трубкою і заповнені сумішшю водню та азоту. У рівновазі в обох судинах буде одна і та ж суміш. Але якщо підігрівати одну посудину і охолоджувати інший (накласти на систему потік негативної ентропії), то почнеться поділ газів. Коли система досягне стаціонарного стану (температура і концентрація перестануть змінюватися в часі), в гарячому посудині виявиться більше водню, а в холодному більше азоту, причому різниця концентрацій буде пропорційна накладеної на систему різниці температур, яка є в даному випадку керуючим параметром. Нічого іншого в цій системі відбутися не може (за винятком того, що, якщо перестати штучно підтримувати різниця температур, то система повернеться в стан термодинамічної рівноваги, що характеризується однорідною сумішшю в обох судинах).
Системи такого роду називаються лінійними, оскільки відбуваються в них зміни лінійно залежать від змін керуючого параметра. Для таких систем можливе правильне передбачення їх поведінки в будь-який момент майбутнього часу.
Цей приклад типовий. На відміну від лінійних моделей, всі приватні рішення яких можна об'єднати в одне загальне рішення (принцип суперпозиції), нелінійні моделі мають не просто різні, а альтернативні рішення, які не можна реалізувати одночасно. Перехід від однієї альтернативи до іншої, що викликається обміном стійкістю, відображає наявність потенційної складової у складного об'єкта.
Складний об'єкт, таким чином, здатний змінювати закони своєї поведінки. Значення керуючого параметра, при якому відбувається зміна поведінки складного об'єкта, називається критичним.
Для ілюстрації зв'язку між нелінійністю і критичністю розглянемо найпростіше рівняння стану
йх
- = А-І, (!)
де X - мінлива стану, до - параметр, А - зовнішнє обмеження на систему. Стаціонарне стан Х $ визначається рівністю нулю правій частині (4), тобто рівністю
* Gt; 4lt; 2gt;
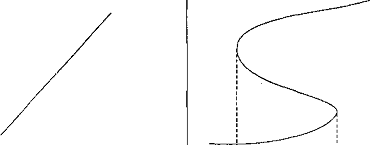
Таким чином, Х5 лінійно залежить від Л, і для кожного значення А є одне і тільки одне значення Х5. На ХА-діаграмі залежність Х5 від А виражається прямою лінією, що проходить через початок координат (рис. 1а). Оскільки для побудови прямої лінії достатньо двох точок, то можна знати Хв для кожного А, маючи дві емпіричні точки (X, 1, А [) і (X, 2, Аг).
У нелінійному випадку замість правої частини (2) повинна бути записана деяка нелінійна функція від А. Найпростіший графічний вигляд нелінійної залежності X, від А дає рис. 16). Якщо А lt; аЬ або А gt; \ -2, то ситуація аналогічна лінійної: єдиній значенням А відповідає єдине значення Х8. Однак, коли А1 lt; А lt; Аг, то одному і тому ж значенню А відповідають декілька різних значень Х5
Точки А1 і Аг є критичними, і в околиці цих точок відбувається біфуркація - замість єдиного способу поведінки системи (єдиного значення Х8) з'являється кілька альтернативних рішень (можливих значень Х8 при даному А), між якими можливий обмін стійкістю.
Така ситуація істотно відрізняється від лінійної. У лінійних системах, якщо А отримує малий приріст ТАК, змінна
а)
Малюнок
стану зміниться на малу величину (у нашому прикладі на ДХ / к). У нелінійних системах навіть малі зміни Л в околиці критичних точок можуть призвести до значних змін у поведінці системи (переходу в альтернативний режим поведінки).
Критичних точок стає більше, коли є кілька управляючих параметрів. У цих випадках можуть з'явитися критичні поверхні і критичні простору.
Властивості нелінійності і критичності проявляються зазвичай у ситуаціях нерівноваги. Для ілюстрації цього твердження найпростіше використовувати термодинамічні уявлення.
Відомо, що для ізольованих систем другий початок термодинаміки стверджує, що
де Б - ентропія системи. Якщо при цьому виконується рівність
то ізольована система знаходиться в состоянии.термодинамического рівноваги і не еволюціонує. В іншому випадку, коли
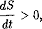
Формула
(5)
ізольована система еволюціонує до стану рівноваги, в якому ентропія максімальна.В відкритих системах, що обмінюються із середовищем енергією і речовиною, крім процесів, що задовольняють співвідношенням (3) - (5), можливі альтернативно протікають еволюційні нерівноважні процеси, для яких
йБ
Л lt; (6)
У таких процесах виникають явища критичності і біфуркації. Тим самим «нерівновагу виявляє потенційні можливості, що містяться в нелінійних і як би" дрімають "в рівновазі або поблизу нього» (Николис і Пригожин, 1989, с. 74).
Динамічний хаос і «власний час». Складні об'єкти мають і інші принципово важливі особливості. Поведінка простих об'єктів строго детерміноване і передбачувано. Типовим прикладом такої поведінки служить другий закон динаміки Ньютона: прискорення-ня пропорційно силі. Якщо відомі всі початкові умови, \?) То 0 помошью цього закону можна як завгодно точно передбачати ^ рух, причому на як завгодно великий час вперед (глобальна ^ детерміністічност').
~ Характеризуючи такі системи за допомогою гамільтоніані, можна ^ "представити кожне їх стан точкою в 67У-вимірному фазовому про-I странстве. Початкова точка і гамильтониан Н повністю визначають ^ траєкторію. Тому будь-які дві траєкторії у фазовому просторі, що виходять з різних початкових точок, завжди будуть різними, ніколи не будуть перетинатися і не зіллються. Кожна точка фазового простору належить одній і тільки одній траєкторії.
Опис такої системи є «грубим»: воно вірно-не тільки для даної конкретної ситуації, але і для всього класу подібних ситуацій. У фазовому просторі стан грубої системи задається не крапкою, а областю. Всі крапки в цій області відповідають «однією і тією ж» системі і зазнають однакові зміни.
Все це змінюється, якщо поведінка динамічних систем допускає нестійкість і тим самим наявність потенційної структури, між прихованими альтернативами якої відбувається обмін стійкістю (нестійкістю). Нестійкість призводить до того, що строго детермінована поведінка поступово стає непередбачуваним. Відрізок часу, протягом якого рух залишається передбачуваним, називається горизонтом видимості. При наявності нестійкості горизонт видимості стає кінцевим.
Замість грубості опису виникає чутливість до початкових умов через те, що спочатку близькі траєкторії з часом експоненціально розходяться. В результаті виникає динамічний хаос:., В-ххрош. -Детермінований них системах, всі стани
Д '! /
наукова бібліотекакоторих однозначно визначаються рівняннями руху і початковими умовами, з часом може виникнути поведінку, неотличимое від випадкового. Справа в тому, що, хоча кожна траєкторія в такій системі строго детермінована, її кінцеві траєкторії, цілком розташовуючись в обмеженому обсязі фазового простору, завдяки локальної нестійкості переплітаються один з одним і перемішуються зразок того, як тасуються карти в колоді. Це і породжує випадкове поводження (за межами горизонту видимості).
Виникнення динамічного хаосу є наслідком наявності потенційної складової, але формально воно пов'язане з нелінійністю системи. «З точки зору математики у всіх нелінійних динамічних системах з числом ступенів свободи більше 2 (особливо у багатьох біологічних, метеорологічних і економічних моделях) можна виявити хаос і, отже, на досить великих часах їх поведінка стає непередбачуваним» (Шустер, 1988, с. 10].
Цікаво, що хаотичні динамічні системи мають явно виражене власний час. Розбігання траєкторій в хаотичній системі описується функцією ехр (? / Т), де 1 / т gt; 0 для хаотичних систем. Величина 1 / т називається показником Ляпунова, а т - часом Ляпунова. Час Ляпунова дозволяє ввести внутрішній «маськи; 'часу» для хаотичних систем.
Кінцевий горизонт видимості і власний час притаманні не тільки хаотичним системам. Вони характерні для будь-яких складних об'єктів, в тому числі що відносяться до соціоекономічної сфері.
1.2
Інформація, релевантна "1.1. Потенційна реальність"
- Передмова
потенційності. Концепція потенційності виходить з дуалізму (подвійності) реального існування, його розділеності на потенційну і акуталізована реальності. Властивості цих реальностей принципово різні. Потенційна реальність являє собою цілісне (що не має частин і тому не володіє причинно-наслідковими зв'язками і просторово-часовими характеристиками) - Леонтьєв Д.А.. Психологія сенсу: природа, будова і динаміка смислової реальності. 2-е, испр. вид. - М.: Сенс. - 487 с., 2003
- Перехід до наступної частини
реальність абсолютного поняття бога, який у якості абсолютної єдності цих обох його моментів є абсолютний дух. Визначеність одного боку відповідає іншій стороні, вона є всепроникна загальна форма, в яку поміщена ідея і яка водночас становить щабель у тотальності її розвитку. Що ж до ступенів реалізації, то в попередньому викладі було вже - Проблема буття і сучасність.
реальності не збігається ні з світом людських цінностей, ні з природою. Ця реальність, дана у мисленні, але, тим не менш має об'єктивне доказові значення. У тлумаченні цієї реальності філософи розділилися на кілька принципово різних течій. Одні стверджують, що буття відкриває справжній світ сутностей і є вікном, що дозволяє поглянути зі світу явищ на - Проблеми структурної організації буття в контексті сучасної науки
потенційно (віртуально) вакуум містить всі можливі частинки і стану, які можуть бути породжені ним за наявності відповідних умов. Вакуум, вважають сучасні фізики, «кишить" не народженими (віртуальними) частками. Саме зважаючи на ці своїх особливостей він виявляється зовсім не самим «бідним», а, навпаки, потенційно самим «багатим» видом буття. До визнання такою воістину - § 2. Що є об'єктом і предметом філософського пізнання?
реальність, в межах якої і протікає-людське життя. Що таке реальність? Реальність - це все те, що існує в явному і неявному вигляді, і тому вона часто іменується буттям. Проявлене для тілесних почуттів людини буття найчастіше іменується дійсністю, а Непроявлена частина буття - реальністю. Дійсність завжди очевидна і тому унікальна, а це означає, що вона - Чому відповідає реальність?
реальності, яка, в свою чергу, є основою для структури мови. Свої ідеї він представив у вигляді знаменитого трактату, названого автором «Логіко-філософським». Написання цієї роботи дало поштовх до розвитку логіки. Вона вплинула на мі-/ ^ Sy филосо-факт світогляду знаменитого «Віденського ^ VE л (4 гуртка» (про який мова піде в - Росія як ядро потенційної альтернативи
потенційний плацдарм для організації прийдешньої альтернативи американської глобальної домінації, лежить в центрі інтересів американської стратегії. Колишні советологіческіе центри часів «холодної війни» сьогодні перейменовуються в центри євразійських досліджень. Євразія і є загальна назва для всієї сукупності «нових викликів» на стратегічному рівні, ядро і полюс вірогідною асиметрії. - Судовий розгляд (початковий етап)
потенційних присяжних на співбесіду. Вони обираються навмання зі списку законослухняних громадян і 12 з них будуть викликані на лаву присяжних для перевірки на неупередженість. Сучасне законодавство в окремих країнах допускає участь 6 присяжних засідателів при розгляді деяких справ. Таке законодавство визнано конституційним Верховним судом. Слід зазначити, що деякі - Способи бути
реальність - це єдина субстанція, що включає в себе Бога і природу. Все існуюче є частина цієї субстанції, яка здатна мислити (віталізм). ? Декарт. Фізична реальність розвивається згідно механічним. принципам. Крім того, існує реальність духовна, до якої відносяться душа людини і Бог. Вона здатна мислити (дуалізм). Дуалізм Декарта допускає чітке розмежування - 1.5. Подання про геополітичні кодах
потенційних загроз. Геополітичні кодекси не просто державно центричний, вони також включають особливий погляд на світ. Одночасно кодекси сприймаються як основні будівельні блоки геополітичних світових порядків. Геополітичні кодекси діють на трьох рівнях - місцевому, регіональному та світовому: 125 Розділ I. Геополітика - Кодекс місцевого рівня складається з оцінок сусідніх - 3.5.1 Аналіз ринку
потенційних покупцях; положенні на ринку і його кон'юнктури; Немає нічого ошибочней, ніж думати, що гідності вашого товару настільки очевидні, що його захочуть купити всі підприємства тієї чи іншої галузі. Аналіз необхідно почати з оцінки потенційної ємності ринку, тобто загальної вартості товарів, які покупці певного регіону можуть 61 купити за певний період часу. Вона - § 10. Які концепції можуть представляти абсолютну, об'єктивну, відносну і конкретну істини?
реальності, а отже, початкове іью і максимальної широтою охоплення. Об'єктивна штші теоретична, бо, намагаючись універсальним оора.юм вони а п. мінливу реальність, задає парадні м \. оорааеп для всіх областей теоретичного мислення. II кові ж істина конкретна у своїй обьекіпвіюсіп і об'єктивна в своїй конкретності. Таке сочеіаппе ми ЖСТ спиратися тільки на закон, що описує - Платон (427-347 рр.. До н. Е..)
реальності я повинен відмовитися від чуттєвого сприйняття. Тому що реальне знаходиться поза чуттєвого і може бути осягнуте тільки розумом. Філософія - це захоплююча подорож, що має метою таке осягнення. Методом просування до невловимої реальності є діалектика. ? Участь? Філософський акт був би неповним, якби він обмежився тільки затвердженням існування - 5. ВІДПОВІДЬ ВІД ІНШИХ свідомості (Йейл)
реальність і пізнаваність ментального точно так само, як у фізичних науках повинно припускати реальність н познаваемость фізичних - Глава перша
потенційністю, якої у вчених речей немає. - 249. 3 І, слід додати, розташовані па одній стороні проходить через неї прямій. - 249. 4 Положення, що сума кутів в трикутнику дорівнює двом прямим. - 249. 5 Потепціальпо пізнаване залежить від позпанія тому, що через останнє воно виявляється, по кожен індивідуальний акт пізнання, в свою чергу, є щось - 4. Висновок: "Позачасовість" і "чар" метафора.
реальність (наприклад: опис філософських поглядів різних філософів). Метафора - те, що з'єднує дві розбіжні філософії: класичну (наприклад, Гегеля) і некласичну (наприклад, "філософію підозри" Ніцше, Маркса або Фрейда). Гегель дає логічну метафору; Ніцше бачить християнство як перевернутий resentiment; Маркс - людини як homo economicus; Фрейд - культуру як